Обчислити визначник, розклавши його за елементами: а) 2-го рядка;

б)1-го стовпця;

в)отримавши попередньо нулі в 2-му рядку

1 2 3 4

А = 0 -1 2 1

2 1 7 9

3 8 10 13

Обчислити визначник, розклавши його за елементами: а) 2-го рядка;б)1-го стовпця;в)отримавши попередн

Показать ответ

Ответ:

nataliarianna29

18.06.2022 11:05

1) нет

2) делящимуся на 5

3)не всегда можно привести к знаменатель 35, так как не все числа делятся на 7(35=5*7). но всегда можно к 25.

4)наименьшее число которое я вляется делимым для двух и более чесел то есть знаменателей

5)надо найти наименьшее целое число на которое делились бы обо (и более) знаменателей

6)методом подбора

7)привести к общему знаменателю

8)привести к общему знаменателю

9)сначало привести к неправильной дроби потом привести к общему знаменателю, сложить и по возможности выделить целуу часть

0,0(0 оценок)

Ответ:

arino4ka3210

08.04.2020 01:39

Пусть х - скорость первого комбайнера, y - скорость второго комбайнера, z - скорость третьего комбайнера. Всю работу обозначим за А.

Исходя из второго предложения можно написать

8x+8y=A.

Третье предложение выражается так

6y+6z=A

Четвертое предложение

12x+12z=A.

Получаем систему

$\begin{cases} 8x+8y=A\\6y+6z=A\\12x+12z=A \end{cases}$

или по-другому

$\begin{cases} x+y=\frac{A}{8},\\y+z=\frac{A}{6},\\x+z=\frac{A}{12}. \end{cases}$

Если сложим все уравнения в этой системе, то получим

$2x+2y+2z=\frac{A}{8}+\frac{A}{6}+\frac{A}{12}$

$2*(x+y+z)=\frac{A}{8}+\frac{A}{6}+\frac{A}{12}$

Поделим обе части на 2

$x+y+z=\frac{A}{16}+\frac{A}{12}+\frac{A}{24}$

$x+y+z=\frac{A}{16}+\frac{2*A}{24}+\frac{A}{24}$

$x+y+z=\frac{A}{16}+\frac{2*A+A}{24}$

$x+y+z=\frac{A}{16}+\frac{3*A}{24}$

$x+y+z=\frac{A}{16}+\frac{A}{8}$

$x+y+z=\frac{A}{16}+\frac{2A}{16}$

$x+y+z=\frac{A+2A}{16}$

$x+y+z=\frac{3A}{16}$

Умножим обе части на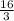 $\frac{16}{3}$ .

$\frac{16}{3}*(x+y+z)=A$

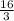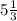Вобщем, требовалось найти за какое время все три комбайна вместе выполнят всю работу. В последней формуле как раз это и видно. Три комбайна (x+y+z) выполняют всю работу А за $\frac{16}{3}$ часа. То есть за $5\frac{1}{3}$ часа. Или по-другому за 5 часов 20 минут.