Математика: ОЧЕНЬ НУЖНА ответ на всё)

ОЧЕНЬ НУЖНА ответ на всё)

Показать ответ

Ответ:

Loomina

10.10.2021 00:08

$2 \ln 8 - 4 + \pi.$

Пошаговое объяснение:

Для вычисления интеграла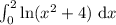 $\int_0^2 \ln (x^2 + 4)\ \text d x$ воспользуемся сначала методом интегрирования по частям:

$u = \ln (x^2 + 4);\ \text d v = \text d x;\\\text d u = \frac{2x}{x^2 + 4}.\ \ \ \ \ \,\,\: x = \int \text d x = x.$

$\int_0^2 \ln (x^2 + 4)\ \text d x = \left \left( x \ln (x^2 + 4) \right) \right | \limits_0^2 - \int_0^2 \frac{2x^2}{x^2+4}\ \text d x.$

Заметим, что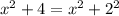 x^2 + 4 = x^2 + 2^2 , и тогда в интеграле после интегрирования по частям напрашивается такая замена:

Если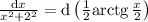 $\frac{\text d x}{x^2 + 2^2} = \text d \left( \frac 12 \text{arctg}\, \frac x2 \right)$ , то, положив 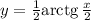$y = \frac 12 \text{arctg}\, \frac x2$ , найдём, что:

$y = \frac 12\, \text{arctg}\, \frac x 2;\\2y = \text{arctg} \frac x 2;\\\text{tg}\, 2y = \frac x 2;\\x = 2\,\text{tg}\, 2y.$

Применим это всё при вычислении получившегося интеграла.

Пределы интегрирования изменятся так:

$a = \frac 12\, \text{tg}\, \frac 0 2 = \frac 12\, \text{tg}\, 0 = 0 \cdot \frac 12 = 0.$

$b = \frac 12\, \text{tg} \frac 2 2 = \frac 12\, \text{tg} \, 1 = \frac 12 \cdot \frac{\pi}{4} = \frac{\pi}{8}.$

Вычислим теперь сам интеграл:

$\int_0^\frac\pi 8 2 \left( 2\, \text{tg}\, 2y \right)^2 \text d y = 8 \int_0^\frac \pi 8 \, \text{tg}^2\, 2y\, \text d y.$

Введём замену: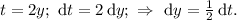 $t = 2y;\ \text d t = 2\, \text d y;\ \Rightarrow\ \text d y = \frac 12\, \text d t.$

Пределы интегрирования изменятся так:

$a = 2 \cdot 0 = 0;\\b = 2 \cdot \frac \pi 8 = \frac \pi 4.$

Продолжим вычисление интеграла:

$4 \int _0^\frac \pi 4\, \text{tg}^2 \, t\, \text d t = 4 \int_0^\frac\pi4 \frac{\sin^2t}{\cos^2t}\, \text d t = 4 \int_0^\frac\pi4 \frac{1 - \cos^2 t}{\cos^2 t} \text d t= 4 \left( \int_0^\frac\pi 4 \frac{\text d t}{\cos^2 t} - \int_0^\frac\pi4\text d t \right) =\\= 4 \left( \text{tg}\, t |_0^\frac\pi4 - t|_0^\frac\pi4 \right) = 4 \left( \text{tg}\, \frac\pi 4 - \text{tg}\, 0 - \frac\pi 4 + 0 \right) = 4 - \pi.$

Подставим найденное значение в выражение после интегрирования по частям и найдём итоговый результат:

$2\ln(2^2 + 4) - 0 \ln (0^2 + 4) - (4 - \pi) = 2 \ln 8 - 4 + \pi.$

Наконец, получаем, что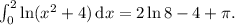 $\int _0^2 \ln (x^2 + 4)\, \text d x = 2 \ln 8 - 4 + \pi.$

0,0(0 оценок)

Ответ:

kgrintsewi4

17.12.2022 10:25

за 8 дней была закончена оставшаяся часть работы

Пошаговое объяснение:

Задание на обратную пропорциональность.

Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.

Через 5 дней 20 рабочих должны закончить всю работу за 10 оставшихся дней.

Через 5 дней количество рабочих стало 25 человек и закончить работу они должны за х дней:

20 раб. - 10 дн

25 раб. - х дн

Составим обратную пропорцию:

20 : 25 = х : 10

х = 20*10/25 = 200 : 25 = 8 дней - за 8 дней была закончена оставшаяся часть работы

0,0(0 оценок)

Популярные вопросы: Математика