Қолтырауын Гена мен Чебурашка екеуі бірдей кубиктер арқылы кубиктер саны тең болатын пішіндер құрастырды. Сол жақта Крокодил Генаның құрастырған пішіні кескінделген де, оң жақта Чебурашканың пішінінің бір қабаты көрсетілген. Чебурашканың пішіні неше қабаттан тұрады?
Пошаговое объяснение:
Точка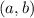 на комплексной плоскости изображает число
на комплексной плоскости изображает число 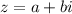
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа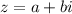 будет являться число
будет являться число 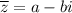 .
.
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси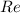 ).
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Приведение к стандартному виду:
\begin{gathered}\displaystyle 2,\!1 \cdot a^2 b^2 c^4 \cdot \bigg ( - 1\frac{3}{7} \bigg ) \cdot bc^3 d = - \bigg ( \frac{21}{10} \cdot \frac{10}{7} \bigg ) \cdot a^2 \cdot b^2b \cdot c^4c^3 \cdot d = = - \frac{21}{7} \cdot a^2 \cdot b^{2+1} \cdot c^{4+3} \cdot d = \boxed {- 3a^2 b^3c ^7d}\end{gathered}2,1⋅a2b2c4⋅(−173)⋅bc3d=−(1021⋅710)⋅a2⋅b2b⋅c4c3⋅d==−721⋅a2⋅b2+1⋅c4+3⋅d=−3a2b3c7d
Коэффициент одночлена: \boxed {-3}−3 .
Задание 2.
Формула для нахождения объема прямоугольного параллелепипеда (VV - объем; xx , yy , zz - измерения прямоугольного параллелепипеда): V=xyzV=xyz .
Значит, объем исходного параллелепипеда равен:
\begin{gathered}V = \Big (4a^2b^5 \Big ) \cdot \Big (3ab^2 \Big ) \cdot \Big (2ab \Big ) = \Big (4 \cdot 3 \cdot 2 \Big ) \cdot a^2aa \cdot b^5b^2b = = 24 \cdot a^{2+1+1} \cdot b^{5+2+1} =\boxed {24a^4b^8}\end{gathered}V=(4a2b5)⋅(3ab2)⋅(2ab)=(4⋅3⋅2)⋅a2aa⋅b5b2b==24⋅a2+1+1⋅b5+2+1=24a4b8