Определи наименьший номер, начиная с которого все члены последовательности (xn) будут не меньше заданного числа A:

xn=3n2−31, A=−3.

ответ:

1. выбери соотношение, необходимое при решении задачи:

3n2−31≥−3

3n2−31≤−3

3n2−31>−3

​

Пусть первая труба пропускает литров. Тогда вторая 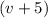л. Если мы вычтем из более производительной трубы мене производительную, то получим время, которое требуется второй трубе, когда первая труба уже заполнила резервуар. Это время по условию равно 10 мин:

Второй корень явно отрицателен, поэтому он нам не подходит, т. к. скорость/производительность — величина положительная.

Тогда вторая труба по условию пропускает 10+5=15 л/мин

ответ: 1-я труба — 10 л/мин, 2-я труба — 15 л/мин.

Проверка: первая труба заполнит первый резервуар за 150:10=15 мин.

Вторая труба за 75:15=5 мин. Мы видим, что первый резервуар заполняется на 10 минут дольше, что и требовалось доказать.

Правильно пишется «рЕшите» и «сИстема»

{ 7(3x+2)-3(7x+2) > 2
{ (x-5)(x+8) < 0

{ 21x + 14 - 21 x - 6 > 2
{ (x^2 - 5х + 8х - 40 < 0

{ 8 > 2 - сомнений не вызывает.
{ x^2 + 3х - 40 < 0

Решим второе неравенство.
Вначале Найдем его корни, приравняв его левую часть к нулю:
x^2 + 3х - 40 = 0
D = 3^2 - 4•(-40) = 9 + 160 = 169
√D = √169 = 13
х1 = (-3 + 13)/2 = 5
х2 = (-3 - 13)/2 = -8
Итак, второе уравнение можно преобразовать как:
(х-5)(х+8) < 0

Решаем методом интервалов:
-∞___+__-8 ___-___0__-__5___+___ ∞

Видно, что неравенство меньше 0 в промежутке (-8; 5)

Следовательно,
-8 < х < 5
или, иначе говоря,
х ∈ (-8; 5).

ответ: х ∈ (-8; 5)