Обозначим радиус основания конуса как R, а его высоту как h. Так как осевое сечение конуса всегда является равнобедренным треугольником, то легко найти гипотенузу такого треугольника, которая, по совместительству, будет являться и 2R:
Зная радиус конуса и один из катетов легко найти высоту:
Вспомним формулы на объем и площадь конуса (V - объем, S - площадь, l - катет прямоугольного треугольника):
ответ: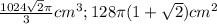
Пошаговое объяснение:
Обозначим радиус основания конуса как R, а его высоту как h. Так как осевое сечение конуса всегда является равнобедренным треугольником, то легко найти гипотенузу такого треугольника, которая, по совместительству, будет являться и 2R:
Зная радиус конуса и один из катетов легко найти высоту:
Вспомним формулы на объем и площадь конуса (V - объем, S - площадь, l - катет прямоугольного треугольника):
Пошаговое объяснение: