Петя задумал число, сложил его квадрат с его кубом и сообщил полученный результат Васе. Однако Вася не смог однозначно определить Петино число. Какое максимальное число мог задумать Петя? Числа могут быть нецелыми, отрицательными и т.д.
(P.S.: правильный ответ 1/3, но надо доказать)
Пошаговое объяснение:
Пусть Петя задумал число х, тогда число, которое он сообщил Васе -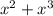 . Так как Вася не смог определить его число, а это значит, что корней у уравнения
. Так как Вася не смог определить его число, а это значит, что корней у уравнения 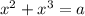 относительно х больше одного.
относительно х больше одного.
Решим это уравнение:
Записав формулу Кардано,
мы получим, что не комплексные корни относительно а - это только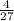 , а для такого значения а относительно х имеется 2 корня -
, а для такого значения а относительно х имеется 2 корня - 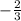 и
и 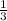 . Наибольший из них конечно же
. Наибольший из них конечно же 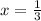 .
.
Если нужно подробно записать формулу Кардано, напишите!