49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле = где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника = = 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
Указать пару точек, которые
имеют одинаковую ординату и
противоположную абсциссу.
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Варианты ответа:
А) М(2; -3), И(2; 3) Б) М(-2; 3), И(2; 3)
В) М(-2; 3), И(2; -3) Г) М(2; -3), И(-2; 3)
Для любой точки (O) сначала указывается
абсцисса (X), а затем -- ордината (Y):
O(X; Y)
Среди вариантов ответа, одинаковую
ординату (3) имеют точки под буквой Б:
Б) М(-2; 3), И(2; 3)
Чтобы они удовлетворяли условию,
они должны иметь противоположные
абсциссы. Числа -2 и 2 являются
противоположными, а значит, они
удовлетворяют условию.
Из этого: правильный вариант
ответа: Б).
49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле =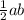
где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника =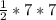
= 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
Указать пару точек, которые
имеют одинаковую ординату и
противоположную абсциссу.
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Варианты ответа:
А) М(2; -3), И(2; 3) Б) М(-2; 3), И(2; 3)
В) М(-2; 3), И(2; -3) Г) М(2; -3), И(-2; 3)
Для любой точки (O) сначала указывается
абсцисса (X), а затем -- ордината (Y):
O(X; Y)
Среди вариантов ответа, одинаковую
ординату (3) имеют точки под буквой Б:
Б) М(-2; 3), И(2; 3)
Чтобы они удовлетворяли условию,
они должны иметь противоположные
абсциссы. Числа -2 и 2 являются
противоположными, а значит, они
удовлетворяют условию.
Из этого: правильный вариант
ответа: Б).