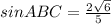запишем условие "Семья состоит из мужа, жены и их дочери студентки." так:
м + ж + д = 100%
м ---доход мужа в %, д ---доход дочери в %, ж ---доход жены в %
2м + ж + д = 100+67
м+м + ж + д = м + 100 = 167 => доходы мужа составляют 67% от дохода семьи
м + ж + д/3 = 100-4
67 + ж + д/3 = 96
д/3 = 96-67 - ж = 29 - ж (умножим на 3)
д = 87 - 3ж ---доходы дочери
вернемся к первому уравнению
67 + ж + 87 - 3ж = 100
2ж = 67+87-100 = 54
ж = 54/2 = 27 ---доходы жены составляют 27% от дохода семьи.
ПРОВЕРКА:
доходы мужа и жены составляют 67+27 = 94% => доходы дочери составляют 6%
если доход дочери уменьшится в 3 раза (составит 6/3 = 2%)
то доходы семьи составят 94+2 = 96% (уменьшатся на 4%)
Чертеж к решению задачи во вложении.Обозначим угол . Требуется найти синус угла АВС, т.е. .
Пусть t- величина одной части при делении стороны ромба точкой касания окружности. Тогда АР=3t, РВ=2t.
По свойству ромба имеем:
1) BD - биссектриса угла АВС;
2) треугольник АОВ - прямоугольный с углом О=90 градусов.
По свойству касательной к окружности ОР-радиус и ОР перпендикуляен стороне АВ.
По свойству высоты прямоугольного треугольника
, т.е.
Тогда ,
В прямоугольном треугольнике ОРВ по теореме Пифагора
В теугольнике ОРВ:
Наконец,
ответ:
запишем условие "Семья состоит из мужа, жены и их дочери студентки." так:
м + ж + д = 100%
м ---доход мужа в %, д ---доход дочери в %, ж ---доход жены в %
2м + ж + д = 100+67
м+м + ж + д = м + 100 = 167 => доходы мужа составляют 67% от дохода семьи
м + ж + д/3 = 100-4
67 + ж + д/3 = 96
д/3 = 96-67 - ж = 29 - ж (умножим на 3)
д = 87 - 3ж ---доходы дочери
вернемся к первому уравнению
67 + ж + 87 - 3ж = 100
2ж = 67+87-100 = 54
ж = 54/2 = 27 ---доходы жены составляют 27% от дохода семьи.
ПРОВЕРКА:
доходы мужа и жены составляют 67+27 = 94% => доходы дочери составляют 6%
если доход дочери уменьшится в 3 раза (составит 6/3 = 2%)
то доходы семьи составят 94+2 = 96% (уменьшатся на 4%)
Чертеж к решению задачи во вложении.Обозначим угол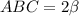
. Требуется найти синус угла АВС, т.е. 
.
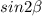Пусть t- величина одной части при делении стороны ромба точкой касания окружности. Тогда АР=3t, РВ=2t.
По свойству ромба имеем:
1) BD - биссектриса угла АВС;
2) треугольник АОВ - прямоугольный с углом О=90 градусов.
По свойству касательной к окружности ОР-радиус и ОР перпендикуляен стороне АВ.
По свойству высоты прямоугольного треугольника
Тогда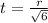
, 
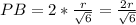
В прямоугольном треугольнике ОРВ по теореме Пифагора
В теугольнике ОРВ:
Наконец,
ответ: