Берем любой из оставшихся шаров, например, зеленый. Его в получившемся ряду мы можем разместить (поставить левее всех, поместить между шарами, поместить правее всех).
Далее, для каждой из образовавшихся последовательностей, следующий, например, желтый шар, мы можем разместить .
Аналогично, для каждой из вновь образовавшихся последовательностей, последний шар мы можем разместить .
Таким образом, число равно:
Также, можно заметить, общее число как-либо разметить 5 шаров равно , причем в половине из них ) красный шар лежит левее синего, а в другой половине красный шар лежит правее синего.
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Изначально расположим красный шар левее синего.
Берем любой из оставшихся шаров, например, зеленый. Его в получившемся ряду мы можем разместить (поставить левее всех, поместить между шарами, поместить правее всех).
Далее, для каждой из образовавшихся последовательностей, следующий, например, желтый шар, мы можем разместить .
Аналогично, для каждой из вновь образовавшихся последовательностей, последний шар мы можем разместить .
Таким образом, число равно:
Также, можно заметить, общее число как-либо разметить 5 шаров равно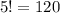
, причем в половине из них ) красный шар лежит левее синего, а в другой половине красный шар лежит правее синего.
ответ: 60
Пошаговое объяснение:
Точка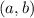
на комплексной плоскости изображает число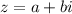 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа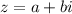
будет являться число 
.
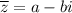В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси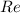
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.