Первую цифру пятизначного числа можно выбрать пятью так как выбираем из чисел 1,2,3,4,5), вторую цифру - четырьмя так как цифры в нашем числе не должны повторяться, а первая цифра уже выбрана), третью цифру - можно выбрать тремя четвертую - двумя, и пятую цифру - одним По правилу умножения (известное в комбинаторике правило) умножаем все для выбора цифр, получаем - 5*4*3*2*1=120 пятизначных чисел.
Далее, кратными пяти могут быть только те числа, которые заканчиваются цифрой 5.
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Пошаговое объяснение:
Первую цифру пятизначного числа можно выбрать пятью так как выбираем из чисел 1,2,3,4,5), вторую цифру - четырьмя так как цифры в нашем числе не должны повторяться, а первая цифра уже выбрана), третью цифру - можно выбрать тремя четвертую - двумя, и пятую цифру - одним По правилу умножения (известное в комбинаторике правило) умножаем все для выбора цифр, получаем - 5*4*3*2*1=120 пятизначных чисел.
Далее, кратными пяти могут быть только те числа, которые заканчиваются цифрой 5.
Пошаговое объяснение:
Точка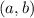
на комплексной плоскости изображает число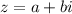 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа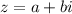
будет являться число 
.
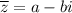В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси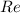
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.