Измерения выполняют при наличии определенных условий, влияющих на их точность. При этом процесс измерений характеризуется рядом факторов, среди которых выделяют: объект измерений, субъект измерений, технические средства, методы измерений и внешнюю среду. Различают следующие погрешности: объекта измерений, связанные с изменением измеряемой величины в процессе измерений, неоднородностью объекта измерений, его нечеткими границами; личные, зависящие от квалификации оператора (исполнителя измерений) и его психологических особенностей; инструментальные, возникающие ввиду невозможности точной юстировки мерного прибора и ограниченности его точности; методы измерений, обусловленные упрощением используемых формул и процессов измерения; внешние, обусловленные влиянием температуры, влажности, освещенности, вибрации и других величин. Любой результат измерения содержит сложную суммарную погрешность, состоящую из большого количества элементарных погрешностей, порождаемых влиянием перечисленных факторов измерений. Измерения считаются равноточными, если все перечисленные факторы и их влияние на процесс измерений примерно одинаковы в течение всего периода производства измерений. При неодинаковых факторах результаты будут неравноточными. Они также будут неравноточными, если условия измерений, характеризуемые рассмотренными выше пятью факторами, будут различаться хотя бы по одному из них.
Все элементарные погрешности измерений классифицируют по двум признакам: источнику происхождения (инструментальные, внешние и личные) и характеру их действия (грубые, систематические, случайные). Грубыми погрешностями называют такие, которые по своей абсолютной величине превосходят установленный для данных условий измерений предел. Они резко отклоняют результаты измерений от действительных значений измеряемых величин и должны обязательно своевременно исключаться. Причиной возникновения грубых погрешностей может оказаться любой из пяти факторов измерений. Чаще всего к такого рода погрешностям относятся промахи в измерениях, вызванные невнимательностью наблюдателя, неисправностью инструмента или неучетом влияния внешней среды, которым нельзя пренебречь. Поскольку исполнитель должен своевременно принимать меры к их недопущению, то естественно, грубые погрешности следует относить к категории личных. Задача исполнителя состоит в организации контроля работ для своевременного устранения из результатов грубых погрешностей. Наиболее действенным методом обнаружения грубых погрешностей является выполнение контрольных измерений тем же инструментом или иным, но той же точности. Поэтому измеряемые расстояния откладывают как минимум дважды.
Но в измерениях всегда остаются погрешности иного рода: систематические и случайные. Систематические погрешности носят так называемый правильный характер, когда при повторных измерениях они либо остаются без изменений, либо изменяются по какому-то определенному закону, либо, изменяясь случайным образом, сохраняют постоянство своего знака. Соответственно различают три вида систематических погрешностей измерения: постоянные, переменные и односторонне действующие. Так, примером постоянной погрешности может служить погрешность измерения ширины колеи подкранового пути, вызванная погрешностью компарирования рулетки, а односторонне действующей — погрешность измерения ширины колеи пути, возникающая из-за неперпендикулярности полотна рулетки, оси подкранового пути. Некоторые систематические погрешности можно устранить из результатов измерения, применив соответствующие методы измерений.
Δx=xa-xb необходимо найти площадь, ограниченную кординатами х=a и x=b
Эта площадь пропорциональна плотности вероятности для интервала Ах.
Если значение случайной величины формируется под действием большого числа взаимно независимых факторов, можно ожидать распределения по так называемому нормальному закону (рис. 3.2). Наибольшая плотность вероятности при нормальном распределении соответствует среднему значению х. По мере того как возрастают отклонения от средней величины, плотность вероятностей быстро убывает. При беспредельном удалении вправо и влево кривая плотности вероятностей асимптотически приближается к оси абсцисс. Для дискретных величин определяют дисперсию
где х — среднее арифметическое значение величины; n — число элементов в выборке.
Если изучается не вся совокупность явлений, а определенная выборка, то дисперсию вычисляют по формуле
где m — число выборочных точек, попавших в i-й интервал.
(-σ...+σ)
(— 3σ... + 3σ)- 0,997
Таким образом, в пределах утроенного отклонения в ту и другую сторону от среднего значения располагается более 99 % всех случаев, а именно 997 из 1000.
До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
Пошаговое объяснение:
1) Производная произведения: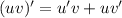
Правило дифференцирования сложной функции: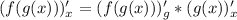
(индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
тогда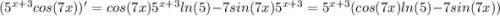
2) Дифференцирование сложной функции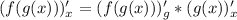
Примем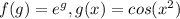
Дифференцируем f(g):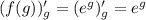
Дифференцируем g(x):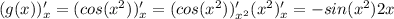
Тогда
3) Как и в 2, дифференцируем сложную функцию
4) Производная суммы есть сумма производных:
Окончательно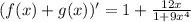
5) Опять производная сложной функции:
Δ=хi-x
Измерения выполняют при наличии определенных условий, влияющих на их точность. При этом процесс измерений характеризуется рядом факторов, среди которых выделяют: объект измерений, субъект измерений, технические средства, методы измерений и внешнюю среду. Различают следующие погрешности: объекта измерений, связанные с изменением измеряемой величины в процессе измерений, неоднородностью объекта измерений, его нечеткими границами; личные, зависящие от квалификации оператора (исполнителя измерений) и его психологических особенностей; инструментальные, возникающие ввиду невозможности точной юстировки мерного прибора и ограниченности его точности; методы измерений, обусловленные упрощением используемых формул и процессов измерения; внешние, обусловленные влиянием температуры, влажности, освещенности, вибрации и других величин. Любой результат измерения содержит сложную суммарную погрешность, состоящую из большого количества элементарных погрешностей, порождаемых влиянием перечисленных факторов измерений. Измерения считаются равноточными, если все перечисленные факторы и их влияние на процесс измерений примерно одинаковы в течение всего периода производства измерений. При неодинаковых факторах результаты будут неравноточными. Они также будут неравноточными, если условия измерений, характеризуемые рассмотренными выше пятью факторами, будут различаться хотя бы по одному из них.
Все элементарные погрешности измерений классифицируют по двум признакам: источнику происхождения (инструментальные, внешние и личные) и характеру их действия (грубые, систематические, случайные). Грубыми погрешностями называют такие, которые по своей абсолютной величине превосходят установленный для данных условий измерений предел. Они резко отклоняют результаты измерений от действительных значений измеряемых величин и должны обязательно своевременно исключаться. Причиной возникновения грубых погрешностей может оказаться любой из пяти факторов измерений. Чаще всего к такого рода погрешностям относятся промахи в измерениях, вызванные невнимательностью наблюдателя, неисправностью инструмента или неучетом влияния внешней среды, которым нельзя пренебречь. Поскольку исполнитель должен своевременно принимать меры к их недопущению, то естественно, грубые погрешности следует относить к категории личных. Задача исполнителя состоит в организации контроля работ для своевременного устранения из результатов грубых погрешностей. Наиболее действенным методом обнаружения грубых погрешностей является выполнение контрольных измерений тем же инструментом или иным, но той же точности. Поэтому измеряемые расстояния откладывают как минимум дважды.
Но в измерениях всегда остаются погрешности иного рода: систематические и случайные. Систематические погрешности носят так называемый правильный характер, когда при повторных измерениях они либо остаются без изменений, либо изменяются по какому-то определенному закону, либо, изменяясь случайным образом, сохраняют постоянство своего знака. Соответственно различают три вида систематических погрешностей измерения: постоянные, переменные и односторонне действующие. Так, примером постоянной погрешности может служить погрешность измерения ширины колеи подкранового пути, вызванная погрешностью компарирования рулетки, а односторонне действующей — погрешность измерения ширины колеи пути, возникающая из-за неперпендикулярности полотна рулетки, оси подкранового пути. Некоторые систематические погрешности можно устранить из результатов измерения, применив соответствующие методы измерений.
Δx=xa-xb необходимо найти площадь, ограниченную кординатами х=a и x=b
Эта площадь пропорциональна плотности вероятности для интервала Ах.
Если значение случайной величины формируется под действием большого числа взаимно независимых факторов, можно ожидать распределения по так называемому нормальному закону (рис. 3.2). Наибольшая плотность вероятности при нормальном распределении соответствует среднему значению х. По мере того как возрастают отклонения от средней величины, плотность вероятностей быстро убывает. При беспредельном удалении вправо и влево кривая плотности вероятностей асимптотически приближается к оси абсцисс. Для дискретных величин определяют дисперсию
где х — среднее арифметическое значение величины; n — число элементов в выборке.
Если изучается не вся совокупность явлений, а определенная выборка, то дисперсию вычисляют по формуле
где m — число выборочных точек, попавших в i-й интервал.
(-σ...+σ)
(— 3σ... + 3σ)- 0,997
Таким образом, в пределах утроенного отклонения в ту и другую сторону от среднего значения располагается более 99 % всех случаев, а именно 997 из 1000.
1212123
4323
δxsup=tσ