а) Вычтем из числа 100...00(Допустим в нём n нулей) число вида 99...99, в котором n девяток , так как кол-во нолей чётно, то и кол-во девяток тоже чётно. Теперь докажем, что в числе вида 99...99(Допустим k девяток), в котором чётное кол-во девяток кратно 11, представим это число в виде суммы 99*10^(k-2)+99*10^(k-4)+...+99 = 99(10^(k-2)+10^(k-4)+...+1). Очевидно, что 99 кратно 11, а значит число вида 99...99(чётное число девяток) кратно 11.
Теперь вычтем из числа 10...00(n нулей) число 99...99(n девяток), очевидно, что разность равна 1, так как 99...99 кратно 11, то разность имеет такой же остаток при делении на 11, как и искомое число. А значит число вида 10...00 с чётным числом нулей при делении на 11 даёт остаток 1.
б) Представим число 10...00 с нечётным числом нулей в виде произведение 10...00(уже с чётным числом нулей) на 10. В пункте а было доказано, что число вида 10...00 с чётным числом нулей даёт остаток 1 при делении на 11. По свойству остатков при умножении числа на какое-то число, то и его остаток умножается на это же число. Из этого следует, что остаток 1 умножается на 10. А значит число вида 10...00 с нечётным числом нулей при делении на 11 даёт остаток 10.
Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида Если a>0, это сразу дает два решения если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна а сумма нечетных равна
Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.
1) Разбиваем на четные и нечетные степени:
найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем
Пошаговое объяснение:
а) Вычтем из числа 100...00(Допустим в нём n нулей) число вида 99...99, в котором n девяток , так как кол-во нолей чётно, то и кол-во девяток тоже чётно. Теперь докажем, что в числе вида 99...99(Допустим k девяток), в котором чётное кол-во девяток кратно 11, представим это число в виде суммы 99*10^(k-2)+99*10^(k-4)+...+99 = 99(10^(k-2)+10^(k-4)+...+1). Очевидно, что 99 кратно 11, а значит число вида 99...99(чётное число девяток) кратно 11.
Теперь вычтем из числа 10...00(n нулей) число 99...99(n девяток), очевидно, что разность равна 1, так как 99...99 кратно 11, то разность имеет такой же остаток при делении на 11, как и искомое число. А значит число вида 10...00 с чётным числом нулей при делении на 11 даёт остаток 1.
б) Представим число 10...00 с нечётным числом нулей в виде произведение 10...00(уже с чётным числом нулей) на 10. В пункте а было доказано, что число вида 10...00 с чётным числом нулей даёт остаток 1 при делении на 11. По свойству остатков при умножении числа на какое-то число, то и его остаток умножается на это же число. Из этого следует, что остаток 1 умножается на 10. А значит число вида 10...00 с нечётным числом нулей при делении на 11 даёт остаток 10.
Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида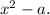
Если a>0, это сразу дает два решения 
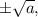если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида 
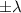я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни 
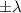тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна 
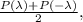а сумма нечетных равна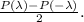 
Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.
1) Разбиваем на четные и нечетные степени: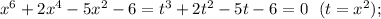
найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем
(t-2)(t+1)(t+3)-2x(t-2)(t+1)=0; (t-2)(t+1)(t-2x+3)=0; (x²-2)(x²+1)(x²-2x+3)=0.
ответ:
2) t³+6t²+11t+6=0; -2x(t^2+3t+2)=-2x(t+1)(t+2)=0;
t³+6t²+11t+6=(t+1)(t+2)(t+3); все уравнение принимает вид
(t+1)(t+2)(t+3)-2x(t+1)(t+2)=(t+1)(t+2)(t-2x+3)=(x²+1)(x²+2)(x²-2x+3)=0.
ответ: решений нет.