Пошаговое объяснение:
Трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Для проверки этих условий вычислим векторы:
АВ=(1-3;2-(-1);-1-2)=(-2;3;-3)
ВС=(-1-1;1-2;-3-(-1))=(-2;-1;-2)
CD=(3-(-1);-5-1;3-(-3))=(4;-6;6)
DA=(3-3;-1-(-5);2-3)=(0;4;-1)
Теперь проверим вычисленные векторы на коллинеарность. Этого достаточно для вывода о параллельности, т.к. координаты точек не совпадают.
Два вектора a и b коллинеарны, если существует число n такое, что
а=n×b.
Как видно из координат векторов, таких вектора у нас 2: АВ и CD, т.к.
АВ×(-2)=СD.
Теперь проверим условие, что длины сторон (т.е. векторов) не равны между собой.
|AB|=
|BC|=
|CD|=
|DA|=
Как видим, ни один из векторов не имеет одинаковую длину с каким-либо другим из четырёх имеющихся.
Все условия соблюдены. Значит АВСD - трапеция.
Пошаговое объяснение:
Трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Для проверки этих условий вычислим векторы:
АВ=(1-3;2-(-1);-1-2)=(-2;3;-3)
ВС=(-1-1;1-2;-3-(-1))=(-2;-1;-2)
CD=(3-(-1);-5-1;3-(-3))=(4;-6;6)
DA=(3-3;-1-(-5);2-3)=(0;4;-1)
Теперь проверим вычисленные векторы на коллинеарность. Этого достаточно для вывода о параллельности, т.к. координаты точек не совпадают.
Два вектора a и b коллинеарны, если существует число n такое, что
а=n×b.
Как видно из координат векторов, таких вектора у нас 2: АВ и CD, т.к.
АВ×(-2)=СD.
Теперь проверим условие, что длины сторон (т.е. векторов) не равны между собой.
|AB|=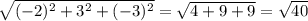
|BC|=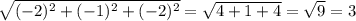
|CD|=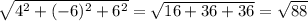
|DA|=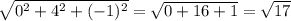
Как видим, ни один из векторов не имеет одинаковую длину с каким-либо другим из четырёх имеющихся.
Все условия соблюдены. Значит АВСD - трапеция.