Расставьте скобки так чтобы получить равенство 2×2+5×2×8-3× 4+7+17=2019​

Уравнение касательной имеет вид:

,

где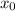 —  абсцисса точки графика функции 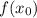, к которому проведена касательная .

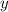Так как график касательной имеет вид график прямой линейной функции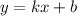 , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —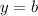

Таким образом, касательная будет горизонтальной, если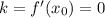

Найдем :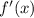

Найдем :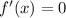

Следовательно,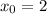 — абсцисса точки графика функции 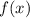, к которому проведена касательная .

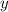Найдем значение :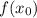

Таким образом,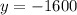 — уравнение горизонтальной касательной к графику функции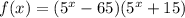

ответ: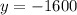

Пошаговое объяснение:

это типо про перенос запятой на десятки

6,4*17=108,8

1)64*17, нужно перенести запятую на один десяток вправо, значит и в ответе тоже перенесется на один десяток вправо

64*17=1088

и таким образом решаем все произведения

2)6,4*170, тут получается тоже самое

6,4*170=1088

3)640*17, здесь переноснится запятая только в первом числе на два десятка, значит:

640*17=10880

4)64*170, здесь переносится в первом на один и во втором на один, в общем на два десятка, значит также как и в предыдущем:

64*170=10880