Математика: Расставьте знаки припепания

Расставьте знаки припепания

Показать ответ

Ответ:

ivonin07

10.01.2020 19:13

Пошаговое объяснение:

для удобства построения графика функции приведем ее в привычный вид квадратичной функции. выделим полный квадрат

0,25х(x+4)-4 = 0

0.25(x² +4x -16) = 0.25(x² +4x +4-20) = 0.25(x+2)²-5

теперь легко построить график

у = 0.25(x+2)²-5

строим у = х², расширяем ветви на 0,25, смещаем график на -2 по оси ох (на 2 влево) и на -5 по оси оу (на 5 вниз.)

теперь определяем точки по оси х, где график <0

целые решения попадают в интервал [-6; 2]

осталось посчитать модули

|-6| + |-5| + |-4| + |-3| + |-2| + |-1| + 0 + |1| + |2| = 24

Используя график квадратичной функции, реши неравенство 1/4(x + 4) –4 < 0 и найди сумму модулей ц

0,0(0 оценок)

Ответ:

SASHEKA

06.03.2021 05:37

Чтобы найти площадь ёлочки, нужно найти площадь верхнего треугольника, площадь центрального прямоугольника и площади прямоугольных треугольничков.

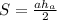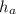Начнём с верхнего треугольника. Чтобы найти его площадь, нужно воспользоваться формулой $S = \frac{ah_a}{2}$ , где - основа треугольника, h_a - высота, опущенная на эту основу. Высота равна 5 клеткам, основа - 7, значит S(треугольничка) =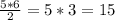 $\frac{5*6}{2} = 5*3 = 15$

Теперь найдём площадь прямоугольника (без того, который находится в верхнем треугольнике) Здесь используем формулу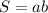 S = ab , где а и b - длинна и ширина. Длина равна 18 клетки, ширина - 2, значит:

S(прямоугольника) =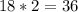 18 * 2 = 36

Перейдём к прямоугольным треугольникам. Они прямоугольные, значит их площадь можно найти по формуле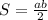 $S = \frac{ab}{2}$ , где a и b - катеты треугольника.

Будем искать площадь начиная нижнего треугольника и заканчивая верхним:

Катет 1: 7

Катет 2: 3

S(прям. треугольника) =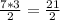 $\frac{7*3}{2} = \frac{21}{2}$

Катет 1: 6

Катет 2: 3

S(прям. треугольника) =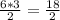 $\frac{6*3}{2} = \frac{18}{2}$

Катет 1: 5

Катет 2: 3

S(прям. треугольника) =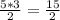 $\frac{5*3}{2} = \frac{15}{2}$

Катет 1: 4

Катет 2: 3

S(прям. треугольника) =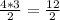 $\frac{4*3}{2} = \frac{12}{2}$

Катет 1: 3

Катет 2: 3

S(прям. треугольника) =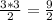 $\frac{3*3}{2} = \frac{9}{2}$

Сложим все эти числа:

$\frac{21}{2} + \frac{18}{2} + \frac{15}{2} + \frac{12}{2} + \frac{9}{2} = \frac{21+18+15+12+9}{2} = \frac{75}{2}$

Здесь мы получили суммарную площадь всех прямоугольных треугольников слева, но не стоит забывать, что справа у нас есть точно такие. Получаем, что суммарная площадь всех прямоугольных треугольников в ёлочке равна:

$\frac{75*2}{2} = 75$