Приравниваем производную (а конкретнее, ее числитель) к нолю:
При этом не дает ноля в знаменателе. Значит, и сама функция, и ее производная, в этой точке существуют.
Теперь, теоремой Виета, найдем точки, в которых функция (и, как следствие, производная) не существует (то есть, знаменатель ⇒ корень из знаменателя равен нолю):
Расставляем знаки производной (на промежутках между числами , и ; точки и - выколотые, а - закрашенная):
+ + + + + + - - - - - -
________________________
И делаем вывод, что точка максимума функции - это .
В ней значение функции равняется:
Задача решена! А график самой функции (нужно сказать, весьма интересный) расположен ниже, во вложении.
Найдем производную:
Приравниваем производную (а конкретнее, ее числитель) к нолю:
При этом не дает ноля в знаменателе. Значит, и сама функция, и ее производная, в этой точке существуют.
не дает ноля в знаменателе. Значит, и сама функция, и ее производная, в этой точке существуют.
Теперь, теоремой Виета, найдем точки, в которых функция (и, как следствие, производная) не существует (то есть, знаменатель ⇒ корень из знаменателя равен нолю):
Расставляем знаки производной (на промежутках между числами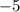 ,
, 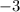 и
и 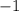 ; точки
; точки 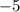 и
и 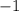 - выколотые, а
- выколотые, а 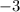 - закрашенная):
- закрашенная):
+ + + + + + - - - - - -
______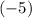 ______
______![[-3]](/tpl/images/1357/3772/c7164.png) ______
______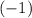 ______
______
И делаем вывод, что точка максимума функции - это .
.
В ней значение функции равняется:
Задача решена! А график самой функции (нужно сказать, весьма интересный) расположен ниже, во вложении.
ответ: - 1 .Пошаговое объяснение:
1.
исследуем по признаку Даламбера
если q < 1, то ряд расходится, если q > 1, то сходится, если =1 неопределенность
ряд сходится
2.
область сходимости ряда это [-R; R], где
у нас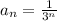
x₁ = 1-3 = -2
x₂ = 1+3 = 4
ряд абсолютно сходится при всех x ∈ (-2;4)
теперь на концах
х = -2
∑ 1/3ⁿ *(-3)ⁿ = (-1)ⁿ
знакочередующийся ряд
по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего.
у нас 1=1=1 - не выполняется.
по второму признаку - предел ряда должен стремиться к нулю (при n стремящейся к бесконечности)
у нас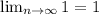
точка х = -2 есть точка расходимости
х = 4
исследуем при интегрального признака сходимости
точка х = 4 так же точка расходимости
3.
тут я не совсем уверена. вот что помню из института....
так что, извините, если что не так