решить через дано AB=BC, BT=4см a) Между какими целыми числами заключена длина отрезка АС? б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.
Рассмотрим функцию . Тогда исходное уравнение имеет вид: .
Заметим, что любой положительный корень уравнения однозначно определяет корень уравнения (это верно в силу того, что уравнение (относительно ) имеет ровно одно решение, так как показательная функция монотонно возрастает на своей области определения). Тогда переформулируем задачу.
При каких значениях параметра , уравнение имеет ровно один положительный корень?
График представляет собой параболу с ветвями вверх.
Исследуем местоположение ее вершины.
.
Заметим, что при любом значении параметра , (это следует из отрицательности дискриминанта). Это говорит о том, что либо у нас вообще нет корней (вершина находится выше оси абсцисс), либо у нас таки есть корень, но он обязательно будет отрицательным.
Для того чтобы мы имели положительный корень, необходимо и достаточно потребовать следующее условие: .
56,9 тонн.
Пошаговое объяснение:
Для того, чтобы ответить на главный вопрос для начала нужно вычислить объём конуса, для чего используем формулу: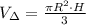 .
.
За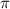 будем считать число 3,14 (хотя для удобства рассчётов больше подошло бы округление до 3, но официально число
будем считать число 3,14 (хотя для удобства рассчётов больше подошло бы округление до 3, но официально число
Не будем также забывать, что диаметр - это два радиуса, поэтому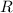 равно 4 м. Теперь считаем объём:
равно 4 м. Теперь считаем объём:
Ну и собственно посчитаем массу:
Рассмотрим функцию . Тогда исходное уравнение имеет вид:
. Тогда исходное уравнение имеет вид: 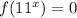 .
.
Заметим, что любой положительный корень уравнения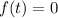 однозначно определяет корень уравнения
однозначно определяет корень уравнения 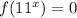 (это верно в силу того, что уравнение
(это верно в силу того, что уравнение 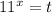 (относительно
(относительно  ) имеет ровно одно решение, так как показательная функция монотонно возрастает на своей области определения). Тогда переформулируем задачу.
) имеет ровно одно решение, так как показательная функция монотонно возрастает на своей области определения). Тогда переформулируем задачу.
При каких значениях параметра , уравнение
, уравнение 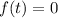 имеет ровно один положительный корень?
имеет ровно один положительный корень?
График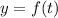 представляет собой параболу с ветвями вверх.
представляет собой параболу с ветвями вверх.
Исследуем местоположение ее вершины.
Заметим, что при любом значении параметра ,
, 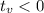 (это следует из отрицательности дискриминанта). Это говорит о том, что либо у нас вообще нет корней (вершина находится выше оси абсцисс), либо у нас таки есть корень, но он обязательно будет отрицательным.
(это следует из отрицательности дискриминанта). Это говорит о том, что либо у нас вообще нет корней (вершина находится выше оси абсцисс), либо у нас таки есть корень, но он обязательно будет отрицательным.
Для того чтобы мы имели положительный корень, необходимо и достаточно потребовать следующее условие: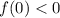 .
.
Тогда имеем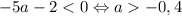 .
.
ответ: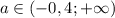 .
.