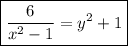Это уравнение с разделяющимися переменными
Получили общий интеграл дифференциального уравнения.
Найдем решение задачи Коши, подставляя начальные условия:
Частный интеграл:
Это уравнение с разделяющимися переменными
Получили общий интеграл дифференциального уравнения.
Найдем решение задачи Коши, подставляя начальные условия:
Частный интеграл: