1) BC =√(15² +20²) =25 ΔCBH (15 ;20 ;25)
AB=√(15² +8²) =17; ΔABH (8;15;17)
R =a*b*c/4S ;
r =S/p , где p полупериметр .
AC=AH +CH =8 +20 =28;
S =(1/2)*AC * BH =14*15 =210 (см²)
R =a*b*c/4S =25*28*17/4*210 = 85/6;
r =S/p ;
p =(17+25+28)/2 =35
r =210/35;
r =6 .
Пошаговое объяснение:
Примечание :
(15 ;20 ;25)= (5*3; 5*4 ;5*5) ; (8;15;17) Пифагорова треугольники
прямоугольные треугольники с сторонами выраж натуральными числами
2) h=32; r=12
R --?
R =a*b*c/4S =ab²/4S.
S =pr
ah/2 =r*(a +2b)/2 ;
a*32 =12(a+2b) (a - , b ).
8a =3(a+2b);
b=5a/6 ;
b² - (a/2)²=12²;
(5a/6)² -(a/2)² =12² ⇒a=18 ;
b=5a/6 =5*18/6 =15.
S=ah/2 =18*32/2 =288
R =a*b*b/4S =18*15*15/4*288 ;
R=225/64.
ЕСЛИ не сложно пометь лутшим
1)
2)
3)
для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.
1-ую строку делим на -3
1 строку * 5 к 2ой добавляем 1 строку
2-ую строку делим на
и последнее 2ую * (2/3) и к 1 строке добавляем 2ую
и вот
4)
определитель матрицы А:
∆A = 1*1 - 2*1 = -1
nак как A невырожденная матрица, то существует обратная матрица A⁻¹
Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹
найдем обратную матрицу A⁻¹.
транспонированная матрица
aлгебраические дополнения
A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;
A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;
обратная матрица
тогда
1) BC =√(15² +20²) =25 ΔCBH (15 ;20 ;25)
AB=√(15² +8²) =17; ΔABH (8;15;17)
R =a*b*c/4S ;
r =S/p , где p полупериметр .
AC=AH +CH =8 +20 =28;
S =(1/2)*AC * BH =14*15 =210 (см²)
R =a*b*c/4S =25*28*17/4*210 = 85/6;
r =S/p ;
p =(17+25+28)/2 =35
r =210/35;
r =6 .
Пошаговое объяснение:
Примечание :
(15 ;20 ;25)= (5*3; 5*4 ;5*5) ; (8;15;17) Пифагорова треугольники
прямоугольные треугольники с сторонами выраж натуральными числами
2) h=32; r=12
R --?
R =a*b*c/4S =ab²/4S.
S =pr
ah/2 =r*(a +2b)/2 ;
a*32 =12(a+2b) (a - , b ).
8a =3(a+2b);
b=5a/6 ;
b² - (a/2)²=12²;
(5a/6)² -(a/2)² =12² ⇒a=18 ;
b=5a/6 =5*18/6 =15.
S=ah/2 =18*32/2 =288
R =a*b*b/4S =18*15*15/4*288 ;
R=225/64.
ЕСЛИ не сложно пометь лутшим
Пошаговое объяснение:
1)
2)
3)
для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.
1-ую строку делим на -3
1 строку * 5 к 2ой добавляем 1 строку
2-ую строку делим на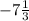
и последнее 2ую * (2/3) и к 1 строке добавляем 2ую
и вот
4)
определитель матрицы А:
∆A = 1*1 - 2*1 = -1
nак как A невырожденная матрица, то существует обратная матрица A⁻¹
Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹
найдем обратную матрицу A⁻¹.
транспонированная матрица
aлгебраические дополнения
A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;
A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;
обратная матрица
тогда