: Пусть МО 1 (ABC). Тогда МО - расстояние от точки M до плоскости квадрата, MO = 6 См. Проведем из точки М перпендикуляры к сторонам квадрата. По условию они равны, значит равны и синие треугольники катету МО. по гипотенузе и общему Тогда точка О равноудалена от сторон квадрата и, значит, О- центр окружности, вписанной в квадрат. Радиус окружности, вписанной в квадрат, равен половине стороны квадрата: OK = 2 см. Из прямоугольного треугольника МОК по теореме Пифагора: MK= sqrt (MO^ 2 +OK^ 2 )= sqrt (36+4) = sqrt 40 =2 sqrt 10 СМ
ответ: 2✓10 см,
Пошаговое объяснение:
: Пусть МО 1 (ABC). Тогда МО - расстояние от точки M до плоскости квадрата, MO = 6 См. Проведем из точки М перпендикуляры к сторонам квадрата. По условию они равны, значит равны и синие треугольники катету МО. по гипотенузе и общему Тогда точка О равноудалена от сторон квадрата и, значит, О- центр окружности, вписанной в квадрат. Радиус окружности, вписанной в квадрат, равен половине стороны квадрата: OK = 2 см. Из прямоугольного треугольника МОК по теореме Пифагора: MK= sqrt (MO^ 2 +OK^ 2 )= sqrt (36+4) = sqrt 40 =2 sqrt 10 СМ
Пошаговое объяснение:
сперва разберемся с первым уравнением системы
log₂(x-y) = 5- log₂(x+y)
представим 5 в виде log₂2⁵
тогда у нас получится
log₂(x-y) = log₂2⁵- log₂(x+y)
или
x² - y² = 32 это первое уравнение нашей системы
теперь рассмотрим второе уравнение
тогда мы имеем
вот в общем-то и всё. дальше чисто вычисления
из второго выражаем х= 12/у и подставляем в первое
z₁=4; z₂ = -36
z₂ нас не интересует, поскольку у₂ не может быть < 0
z = 4 ⇒ y = ± 4
y₁ = -2 x₁ = 12/(-2)= -6 но по определению логарифма должно быть
x >0 b y > 0, значит эта пара корней нам не подходит
y₂ = 2 x₂ = 12/(2)= 6 проверяем на все огараничения
x - y > 0 x > y выполняется
х, у > 0 выполняется
эта пара и есть корни нашей системы
тогда ответ
х₀ + у₀ = 8
зеленый график это уравнение log₂(x-y) = 5- log₂(x+y)
фиолетовый график это уравнение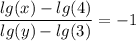
на втором рисунке более общий вид графиков