Решить тесты 2. Вирази 4(а-2) і 4а-8 тотожно рівні?
Так
Ні
3. Після зведення подібних доданків у виразі -3b+4b-2b одержали
9b
b
-b
5b
4. Який з виразів тотожно рівний виразу x+5x
5x
4x
6x
5. Чи є рівність xy+10=10+xy тотожністю?
Так
Ні
6. При спрощенні виразу 2(3а+4)-6а отримали
12
8
4
-12
7. Чи є вираз -(x+6) i (x+6) тотожно рівними
ні
так
8. Виберіть тотожність, яка відповідає твердженню «сума числа і протилежного йому числа дорівнює нулю»
-а • а =0
-а +(-а)=0
а+(-а)=0
9. Ширина прямокутника дорівнює a см, а довжина на 3 см більша від ширини. Виберіть вираз, який тотожно рівний периметру прямокутника
Р=2(а+3)
Р=2(2а+3)
Р=2а+3а
Р=2а+3
10. На одній полиці стоїть n книжок, а на іншій у 3 рази більше. Скільки книжок стоїть на обох полицях?
3n
n+3
4n
11. Знвйдіть значення виразу 12-8х, якщо х=-2.
-4
28
-28
16
12. Який з даних виразів є числовим?
12-8х
-4,5+43,2•(-0,7)
-2а(-18+1,7а)
(23-у)(-1,6)

1. По условию задачи известно, что 6300 билетов составляют 7/9 от всех имеющихся. Возьмем количество всех билетов за х. Составим пропорцию.

6300 = 7/9;

х = 1 (9/9);

х =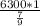 = = 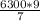900*9 = 8100 билетов (всего). Отсюда вычислим количество билетов, которые осталось продать.

2. 8100 – 6300 = 1800.

Можно было решить эту задачу намного проще: Найдем 1/9 часть от всех билетов, разделив 6300 на 7, получим 900. Тогда количество билетов, которые осталось продать, будет составлять 2/9, а в численном отношении – 900*2 = 1800.

ответ: 1800 билетов.

1. 11х – 9 = 4х + 19

11х – 4х = 19 + 9

7х = 28

х = 4

ответ: х = 4.

2. Пусть за третью неделю отремонтировали х км дороги, тогда за первую неделю отремонтировали 3х км, а за вторую - х+8 км. Известно, что за три недели отремонтировали 58 км дороги, составим уравнение.

х + х + 8+ 3х = 58;

5х = 50;

х = 10. Отсюда, за третью неделю отремонтировали 10 км дороги, за первую - 30 км, за вторую - 18 км.

ответ: 10 км.

3. 5,6 – 3*(2 – 0,4х) = 0,4*(4х + 1)

5,6 – 6 + 1,2х = 1,6х + 0,4

1,6х – 1,2х = 5,6 – 6 – 0,4

0,4х = –0,8

х = –2

ответ: х = –2.

4. Пусть в обоих озерах было по х уток. Когда с первого озера улетели 29 уток (х–29), а со второго – 11 уток (х–11), то на первом озере осталось в 7 раз меньше уток, чем на втором:  

7*(х–29) = х–11;  

7х – 203 = х–11;

6х = 192;

х = 192:6 = 32. Столько уток было на каждом озере изначально.

ответ: 32 утки.

5. 0,6 – 1,6*(х – 4) = 3*(7 – 0,4х)

0,6 – 1,6х + 6,4 = 21 – 1,2х

– 1,6х + 1,2 х = 21 – 0,6 – 6,4

-0,4х = 14

х = -35.

ответ. х = -35.