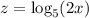Войти Регистрация Спроси ai-bota

Решить уравнение 7log^2_5(2x) - 20log_5(2x) - 3 = 0.

Показать ответ

Ответ:

Nasteckay

15.10.2020 14:30

$\frac{125}{2}, \frac{1}{2\sqrt[7]{5}}$

Пошаговое объяснение:

$7\log^2_{5}(2x)-20\log_5(2x) - 3 = 0.$

Сделаем замену переменной: $z = \log_5(2x)$

7z^2 - 20z -3 = 0;

D = 400 + 84 = 484;

$\left [ {{z=\frac{20+22}{14}} \atop {z=\frac{20-22}{14}}} \right. = \left [ {{z=3 \atop {z=-\frac{1}{7}}} \right.$

$\left [ {{\log_5(2x)=3} \atop {\log_5(2x)=-\frac{1}{7}}} \right. = \left [ {{2x=5^3} \atop {2x=5^{-\frac{1}{7}}}} = \left [ {{2x=125} \atop {2x=\frac{1}{\sqrt[7]{5}}}} = \left [ {{x=\frac{125}{2}} \atop {x=\frac{1}{2\sqrt[7]{5}}}}$

0,0(0 оценок)

Популярные вопросы: Математика

УРОК000

17.11.2021 02:04

Решить ! 1) сыну 24 года возраст его относится возрасту отца , как 2: 4 целых одна ворая. сколько лет отцу? 2) мастер сплавил золото и серебро в отношении 5: 8. золота...

Zayats2007

06.12.2022 23:02

Найдите нод(a,b) и нок(a,b), если : а) а=34*11, б=22*35*72; б)а=22*33*7, б=33*5....

Кристина20060805

06.12.2022 23:02

Пятую часть дистанции петя бежал за 16 секунд с максимальной скоростью 5м/с.затем он снизил скорость и на финише показал время 96 секунд.с какой скоростью петя пробежал...

doda4i

06.12.2022 23:02

Сократить дробь: 5x-5корней из 3 / 3-x в квадрате...

deisika7

06.12.2022 23:02

Решить пример и расставить попядок , ! 40•3: 60+(6•7-7): 5-4: (4-0)•9=...

ARCrafter

06.12.2022 23:02

Примеры техногенных аварий в крыму и севастополе!...

bramekanep0akn0

06.12.2022 23:02

Подскажите художественные произведения ()или кино, в которых главный герой (или герои) выживает в условиях автономного существования а природе. робинзона не надо : )...

SirykValia

06.12.2022 23:02

Школьники определили с опытов такие свойства вещества: белое,непрозрачное,в тепле превращается в воду,рыхлое? с каким веществом работали дети на уроке? какой газ поддерживает...

Mixof

08.08.2021 10:07

Шестизначное число начинается цифрой 5. если переставить эту цифру на последнее место шестизначного числа, то получится число, в 4 раза меньшее первоначального. найди...

знайка56884

08.08.2021 10:07

Два автобуси одночасно і в протилежних напрямках виїхали із сіл ,відстань між якими становить 30 км. перший автобус їхав зі швидкістю 60 км на годину , а другий зі швидкістю...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку