Найдем сначала общее решение соответствующего однородного уравнения:
Пусть , получим характеристическое уравнение:
Рассмотрим функцию
Здесь
Сравнивая α с корнями характеристического уравнения и, принимая во внимания, что n=1, частное решение будем искать в виде:
Подставим в исходное дифференциальное уравнение:
Приравниваем коэффициенты при степенях х:
Частное решение:
Общее решение линейного неоднородного дифференциального уравнения:
Найдем сначала общее решение соответствующего однородного уравнения:
Пусть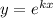 , получим характеристическое уравнение:
, получим характеристическое уравнение:
Рассмотрим функцию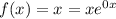
Здесь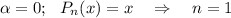
Сравнивая α с корнями характеристического уравнения и, принимая во внимания, что n=1, частное решение будем искать в виде:
Подставим в исходное дифференциальное уравнение:
Приравниваем коэффициенты при степенях х:
Частное решение: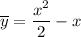
Общее решение линейного неоднородного дифференциального уравнения: