Математика: с математикой разбить каждое число на классы дугами

с математикой разбить каждое число на классы дугами

Показать ответ

Ответ:

marinakoch

13.11.2020 10:43

x1 = 8 м/с и x2 = 10 м/с - в момент времени t1 = 1

x1 = 24 м/с и x2 = 22 м/с в момент времени t2 = 3

Пошаговое объяснение:

Указанные законы

$x_1(t)=4t^2+2 \\ x_2(t)=3t^2+4t-1$

описывают функциональные зависимости расстояния х1 и х2 от времент t

Моментами, когда пройденные точками расстояния равны, будут такие моменты времени t, при которых

будет соблюдаться равенство:

x_1(t) = x_2(t)

Скорости точек v1 ,v2 определяются как производные от функций расстояния в заданные моменты времени t,

$v_1(t) = x_1'(t) \\ v_2(t) = x_2'(t)$

1. Определим моменты времени t, когда выполняется равенство

$x_1(t){=}x_2(t) \: { } \: 4t^2+2 =3t^2+4t-1$

Решим уравнение

$4t^2+2 =3t^2+4t-1 \\ 4t^2 + 2 - 3t^2 - 4t + 1 = 0 \\ t^2 - 4t +3 = 0$

По Т. Виета разбиваем на множители:

$(t - 1)(t - 3) = 0 \\ t_1 = 1\: c \\ t_2 = 3\:c \\$

2. Найдем скорости точек в моменты времени t1 и t2

2а) Определим формулы скорости:

$v_1(t) = x_1'(t) \\ x_1(t)=4t^2+2 \\x' _1(t)=(4t^2+2)' = 4 \cdot2t^{2 - 1} + 0 \\v_1(t) = 8t \\ \\ x_2(t)=3t^2+4t-1 \\ v_2(t) = x_2'(t) \\ v_2(t) = (3t^2+4t-1)' \\ v_2(t) =3 \cdot2t^{2 - 1} + 4 \cdot t^{1- 1} + 0 \\ v_2(t) =6t + 4$

2б) Найдем скорости точек в моменты времени t1 и t2

$t_1 = 1\: c \\ v_1(t) =8t \\v_1(1) =8 \times 1 = 8 \: m/c \\ \\ v_2(t) =6t + 4 \\ v_2(1) =6 \times 1 + 4= 10 \: m/c$

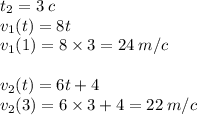
$t_2 = 3 \: c \\ v_1(t) =8t \\v_1(1) =8 \times 3 = 24 \: m/c \\ \\ v_2(t) =6t + 4 \\ v_2(3) =6 \times 3 + 4= 22 \: m/c$

8 м/с и 10 м/с в момент времени t1 = 124 м/с и 22 м/с в момент времени t2 = 3

0,0(0 оценок)

Ответ:

DevA777

10.12.2022 20:04

Y = x² - парабола (на рисунке синяя линия)

х = 3 - прямая перпендикулярная оси абсцисс, проходящая через точку (3,0) (зелёная линия на рисунке)

y = 0 - прямая, совпадающая с осью абсцисс (красная линия на рисунке)

Найдём ещё одну прямую, которая ограничивает параболу по иксу. Для этого в уравнение параболы подставляем y=0 и решаем уравнение относительно икса: x = 0 - ещё одна прямая перпендикулярная оси абсцисс (левая зелёная линия).

В итоге получается область серого цвета, площадь которой надо найти. Площадь находится с определённого интеграла от параболы в пределах от х=0 до х=3 (это будут пределы интегрирования).

Пошаговое объяснение:

0,0(0 оценок)

Популярные вопросы: Математика