Математика: сделать все кроме 1, если можно подробно

сделать все кроме 1, если можно подробно

Показать ответ

Ответ:

Vspichka

26.08.2020 12:53

$x \in (-\frac{\pi}{4}+2\pi k,\frac{\pi}{4} +2\pi k)$

Пошаговое объяснение:

Чтобы произведение двух множителей было положительным они должны иметь одинаковый знак и не равняться нулю.

$\sqrt{cos(x)}$ - всегда неотрицателен когда существует.

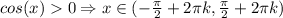Т.е. $cos(x) 0 \Rightarrow x \in (-\frac{\pi}{2}+2\pi k,\frac{\pi}{2} +2\pi k)$ (ноль не рассматриваем)

Т.к. первый множитель (корень) всегда неотрицателен, то второй множитель (скобка) также должен быть положительным.

Т.е.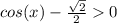 $cos(x) - \frac{\sqrt{2} }{2} 0$

Решаем:

$cos(x) \frac{\sqrt{2} }{2} \Rightarrow x \in (-\frac{\pi}{4}+2\pi k,\frac{\pi}{4} +2\pi k)$

Объединяем условия: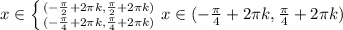 $x \in \left \{ {{(-\frac{\pi}{2}+2\pi k,\frac{\pi}{2} +2\pi k)} \atop {(-\frac{\pi}{4}+2\pi k,\frac{\pi}{4} +2\pi k)}} \right. \Rightqrrow x \in (-\frac{\pi}{4}+2\pi k,\frac{\pi}{4} +2\pi k)$

============

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Бодрого настроения и добра!

Успехов в учебе

0,0(0 оценок)

Ответ:

novkov641800

10.12.2020 21:21

Відповідь:

$\frac{1}{n!}$

Покрокове роз'яснення:

Простір елементарних подій (Ω), тобто кількість усіх рівноможливих результатів цього стохастичного (випадкового) експерименту, дорівнює перестановкам із чисел 1, 2, 3, ..., n. (n! послідовностей)

Ну і дійсно: нам же потрібно визначити, які можуть бути різні комбінації із чисел при витягуванні їх для того, щоб дізнатися, скільки є рівноможливих наслідків цього експерименту.

Якщо їх (чисел), до прикладу, буде 3, то нам потрібно визначити скільки є комбінацій із цих чисел без повторень, тобто 3! (для формули потрібно, якщо хтось ще не зрозумів)

Відповідно, кількість усіх рівноможливих результатів деякого стохастичного (випадкового) експерименту, при якому ми б послідовно витягували усі числа, пронумерованих як 1, 2, 3, ..., n, дорівнюють кількості перестановок із цих чисел, тобто n!

Сприятлива подія полягає в тому, що при витягуванні послідовно n чисел, послідовність вийде зростаючою. Така подія 1 - вона і є сприятливою.

То тепер, нехай A - це подія, при якій утвориться зростаюча послідовність, а P(A) - її ймовірність. Тоді:

$P(A) = \frac{m}{b}$ , де b - кількість рівноможливих наслідків цього експерименту (n!), а m - це наслідки події A, тобто сприятливі події (1).