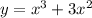Сделайте Исследовать на экстремум функцию y=x³+3x² - вопрос №313461997 от Dorefi 30.01.2020 16:27

Question

Математика: Сделайте Исследовать на экстремум функцию y=x³+3x²

Dorefi · Answer

1).

Для того, чтобы исследовать функцию y=x^3+3x^2 , найдем ее производную:

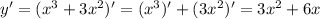
y' = (x^3+3x^2)' = (x^3)'+(3x^2)' = 3x^2+6x

2).

Приравняем производную к нулю и найдем абсциссы точек экстремума:

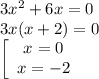
$3x^2+6x=0\\3x(x+2)=0\\\left[\begin{array}{ccc}x=0\\x=-2\end{array}\right$

3).

Исследуем знаки производной:

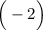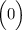+++++++++++++++ $\Big (-2 \Big)$ --------------- $\Big ( 0 \Big )$ ++++++++++++++

Значит:

На промежутке $( - \infty; -2]$ функция возрастает.

На промежутке [-2;-1] функция убывает.

На промежутке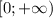 $[0;+ \infty)$ функция возрастает.

4).

Найдем критические значения функции.

В точке максимума ( x=-2 ):

$y = x^3+3x^2 = (-2)^3+3 \cdot (-2)^2 = -8 + 12 = 4$ .

В точке минимума:

$y = x^3+3x^2 = 0^3 + 3 \cdot 0^2 = 0$ .