Сделайте только четные

64

Пошаговое объяснение:

Один из видов решения, заключается в использовании метода Гаусса и в составлении квадратного уравнения. 1 - одно число, 2 - два числа, 3 - три числа и так далее 10 - десять чисел, отсюда следует 1+2+3+4+5+6+7+8+9+10 = 55 - пятьдесят пять чисел. По методу Гаусса (1+10)*5 = 55. Заметьте, если бы нам пришлось складывать 11 чисел, то (1+11)*5.5 = 66. Отсюда, при закономерности составим уравнение:

корень из дискриминанта приблизительно равно 127.

Второй корень отрицательный, его брать не будем.

Проверим по этой формуле

. Это означает, что от 1 до 63, количество чисел будет 2016 (1,2,2,3,3,3...63*63). А 2020-е число это 4-ое число 64.

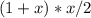
ответ: 64

Пошаговое объяснение:

последовательность выглядит следующим образом

1,2,2,3,3,3,4,4,4,4,    обозначим эту последовательность (1)

составим последовательность из количеств каждого натурального числа встречающегося в этой последовательности

то есть единиц -1,  двоек-2, троек-3,...

1,2,3,4,5,6, обозначим эту последовательность (2)

заметим что сумма одного члена этой последовательности равна количеству единиц последовательности (1)

заметим что сумма двух членов этой последовательности равна количеству единиц и двоек последовательности (1)

и так далее

сумма n членов этой последовательности равна количеству чисел до n (включительно) последовательности (1)

найдем n когда сумма последовательности (2) ≈ 2016  (приближенно)

по формуле суммы арифметической прогресии

Sn=(2a₁+d(n-1))*n/2

a₁=1; d=1

Sn=(2a₁+d(n-1))*n/2=Sn=(2+n-1)*n/2=(n+1)n/2

Sn=2020

(n+1)n/2=2020

n²+n-4040=0 решим квадратное урвнение

d=1+4*4040=1661

√1661=приближенно 127

n=(-1+127)/2≈126/2=63 (рассматриваем только положительный корень)

Найдем точное значение S₆₃=(63+1)*63/2=2016

то есть с 1 по 2016-го места в последовательности (1) идут числа

от 1 до 63 а начиная с 64го места идут числа 64

S₆₄=(64+1)*64/2=2080

так как  2016<2020<2080

то  на 2020 месте стоит число 64