Шестнадцать одинаковых деревянных брусков размерами стоят вместе и образуют большой брус размером 9на4 на4 (высота бруса равна9 ). На каждый из брусков сверху посадили по термиту. Каждый термит начал сверху есть свой брусок. Спустя неделю оказалось, что два термита съели по кубику , два термита съели по кубика , два термита съели по кубика, ..., два термита съели по кубиков . Теперь большой брус выглядит следующим образом (на рисунке изображён вид сверху, спереди и справа).
Сколько кубиков суммарно съели два термита, сидящие на отмеченных на рисунке брусках?

1.

всего - 55 кг

я-?

г-? но на 5  больше я

55-5=50кг

50:2=25кг(яблоки)

25+5=30кг(груши

ответ: груш - 30 кг яблок - 25 кг

2.

всего - 30 книг

1 полка - ? но на 5 книг больше

2 полка - ?

задача не правильная

давайте решим методом подбора:

представим на 1 полке 17 значит на 2 полке 12 при сложение этих чисел получается 29 т.е задача не может быть решена.

3.

всего - 94

1 дн. - ?

2 дн. - ? но на 8 меньше

8:2=4

94:2=47

47-4=43( 2 дн)

47+4=51( 1 дн)

4.

всего - 48

1 класс - ? но 6 меньше

2 класс - ?

6:2 = 3

48:2 = 24

24-3 = 21(во 2 классе)

24+3 = 27( в 1 классе)

Пошаговое объяснение:

Пошаговое объяснение:

Введем замену ; .

Уравнение примет вид

Далее заметим, что для любого верно   . То есть верхнее ограничение выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения 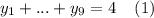 в целых неотрицательных числах.

А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].

Искомое количество вариантов