сколько получится с кр

1. В коробке находятся 20 патронов, из которых 7 – от пистолета Макарова. Найти число различных взятия 5 патронов, из которых 3 подходят к пистолету Макарова.

2. Из урны с 5 белыми и 7 черными шарами наугад берут 4 шара. Найти вероятность, что взято черных шаров больше, чем белых.

3. Вероятность попадания в мишень при 1-ом выстреле 0.4. В случае попадания при 1-м выстреле вероятность попадания при 2-ом выстреле 0.75. В случае промаха при 1-ом выстреле вероятность попадания при 2-ом выстреле 0.5. Найти вероятность того, что при 2-х выстрелах будет 2 попадания.

4. В оружейном шкафу хранятся 6 пистолетов Макарова и 4 пистолета ТТ. Вероятность поражения мишени из пистолета Макарова – 0,7; из пистолетаТТ – 0,8. Какова вероятность поражения стрелком мишени из наугад взятого пистолета?

5. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет не менее двух раз.

6. Вероятность попадания в мишень при одном выстреле - 0,6. Стрельба ведется сериями по 5 выстрелов. Производится 30 серий. Случайная величина X - число серий, в каждой из которой было по 4 попадания. Найти М(X), D(X), s(X).

Показать ответ

Ответ:

Рикон1

16.10.2020 16:13

Пошаговое объяснение:

Первое, что стоит заметить - область определения функции: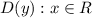 $D(y): x \in R$ .

Функция будет убывать на всей числовой оси (т.е., монотонно убывающей) тогда и только тогда, когда её производная будет неположительной:

$y'(x)=-3x^2+2*2x+a=-3x^2+4x+a \leq 0$ .

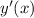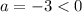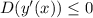График функции y'(x) - парабола, причём направлена ветками вниз ( a=-3 ), а поэтому её область значений всегда будет неположительной, если она не имеет точек пересечения с осью абсцисс или касается её. Отсюда вытекает, что квадратное уравнение не имеет решений или имеет только одно только при $D(y'(x)) \leq 0$ .

$D = 4^2-4*(-3)*a=16+12a \leq 0$ .

Отсюда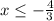 $x \leq -\frac{4}{3}$ .

0,0(0 оценок)

Ответ:

ntaskaeva2

20.11.2020 19:05

1) -36+69+(-17)+(-42)+32=69+(-17-42)+(32-36)=69-59-4=10-4=6

Складывал, используя законы сложения. т.е. менял местами слагаемые и сочетал, как нравилось. Сначала сложил отрицательные, потом с разными знаками во второй скобке. и от первого результата вычел второй.

2) -8-(-12) -(-7)+12-20=-8+12+7+12-20=(-8+7)+(12+12-20)=-1+4=4-1=3

Минус на минус при умножении плюс. раскрыл такие минусы перед 12 и 7, получил положительные, а потом набрал в скобки те числа, которые легко сложить между собой, опять же, используя законы сложения.

0,0(0 оценок)

Популярные вопросы: Математика