Сложение и вычитание десятичных дробей. Вычислите устно (@ 720—725).
720. а) 7 + 0,3;
в) 1,4 + 1,08;
д) 2,1 + 0,05;
N
б) 1,3 + 1,85;
г) 2,03 + 0,8;
е) 1,07 + 1,3.
721. а) 1,8 + 0,5;
в) 1,6 + 2,8;
д) 1,3 + 0,8;
б) 0,7 + 3,9;
г) 0,4 + 4,8;
е) 0,6 + 1,9.
Вычислите устно (752-760).
752. а) 2,3 – 1,4; б) 2,8 - 1,9; в) 4,1 – 2,6; г) 3,6 – 1,8.
753. а) 8,2 – 2,8; б) 7,3 — 3,7; в) 9,1 — 1,9; г) 6,5 – 5,6.
754. а) 7,83 — 5,492; в) 0,9 — 0,521; д) 5 — 0,39;
б) 5,21 – 5,179; г) 89,1 – 8,49; е) 3 – 2,665.ХЕЛППППП(**(​

ответ:  180.  

Вот формула площади трапеции:

, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).

Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен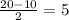 . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:  

Теперь высоту мы знаем и можем найти площадь трапеции:

Задача решена!

y=(x+2)^2+4 - квадратичная функция, график - парабола, ветви направлены вверх, график можно получить путём параллельного переноса графика функции y=x^2 на 2 единичных отрезка влево и на 4 единичных отрезка вниз

1) D(y)=R

2) Нули: x=0 при y=0; y=0 при x=0 и x=-4

3) y<=0 при x принадлежащем [-4;0], y>0 при x принадлежащем (-бесконечность;-4) и (0;+ бесконечность)

4) Функция убывает на промежутке x принадлежащем (-бесконечность;-2) и возрастает на промежутке x принадлежащем (-2;+ бесконечность)

5) E(y)=[-4;+бесконечность).

Пошаговое объяснение: