Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Высота конуса – это перпендикуляр, который опущен из вершины конуса на плоскость основания. Основание высоты в прямом конусе совпадает с центром основания.
Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Треугольник POA вращается вокруг стороны PO.
PO — ось конуса и высота конуса.
P — вершина конуса.
PA — образующая конуса.
Круг с центром O — основание конуса.
AO — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось PO конуса.
Осевое сечение конуса — это равнобедренный треугольник.
APB — осевое сечение конуса.
∡PAO=∡PBO — углы между образующими и основанием конуса.
Образующая конуса, высота и радиус основания образуют прямоугольный треугольник.
Поэтому если известна образующая (гипотенуза) и радиус (катет), то высоту можно выразить с теоремы Пифагора.
Пошаговое объяснение:
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Высота конуса – это перпендикуляр, который опущен из вершины конуса на плоскость основания. Основание высоты в прямом конусе совпадает с центром основания.
Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Треугольник POA вращается вокруг стороны PO.
PO — ось конуса и высота конуса.
P — вершина конуса.
PA — образующая конуса.
Круг с центром O — основание конуса.
AO — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось PO конуса.
Осевое сечение конуса — это равнобедренный треугольник.
APB — осевое сечение конуса.
∡PAO=∡PBO — углы между образующими и основанием конуса.
Образующая конуса, высота и радиус основания образуют прямоугольный треугольник.
Поэтому если известна образующая (гипотенуза) и радиус (катет), то высоту можно выразить с теоремы Пифагора.
a² = c² - b², a = √(c² - b²).
a - высота, b - радиус, c - образующая.
Пошаговое объяснение:
а) Р=4а=4*9=36 см
Обратная задача: периметр квадрата Р=36 см . Чему равна сторона квадрата?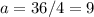 см
см
б) Р=2*(a+b)=2*10=20 см
Обратная задача: периметр прямоугольника Р=20 см, одна из его сторон a=3 см. Чему равна вторая сторона прямоугольника? b=(20/2)-3=7 см
в) Р=4а ⇒ а=Р/4=32/4=8 см
Обратная задача: Сторона квадрата – 8 см. Чему равен периметр? Р=4а=4*8=32 см
г) Р=2*(a+b) ⇒ b=(P/2)-a=14/2-5=7-5=2 см
Обратная задача: стороны прямоугольника – 5 см и 2 см. Найди периметр. Р=2*(a+b)=2*(5+2)=14 см