Стартовали они оба из одной точки и побежали в одну сторону вокруг моря, которое на самом деле было небольшим солёным озером, береговая линия которого в целом составляла 7 км. Средняя скорость зайца на протяжении этого времени составляла 72 км/ч, и через 20 минут после старта он опережал чертёнка на один круг вокруг озера. Какова была скорость чертёнка, которому не следовало тягаться с самим Балдою, раз он не мог догнать его меньшого брата?

Показать ответ

Ответ:

nnn0212

01.01.2021 20:37

Пошаговое объяснение:

$A=\begin{pmatrix} 1&1&-1\\2&-4&1\\4&-3&1\end{pmatrix}, \; B=\begin{pmatrix} 1&0&-4\\2&5&-3\\4&-3&2\end{pmatrix}$

Здесь я позволю себе подробно расписать получение элементов при умножении матриц, но обычно все расчеты проводят усно и так лучше не шутить:)

а)

$BA=\begin{pmatrix} 1&0&-4\\2&5&-3\\4&-3&2\end{pmatrix}*\begin{pmatrix} 1&1&-1\\2&-4&1\\4&-3&1\end{pmatrix}=\\\begin{pmatrix}1*1+0*2-4*4&1*1-4*0-4*(-3)&-1*1+0*1-4*1\\2*1+5*2-3*4&2*1-4*5-3*(-3)&-1*2+5*1-3*1\\4*1-3*2+2*4&4*1-3*(-4)-3*2&-1*4-3*1+2*1\end{pmatrix}=\\\begin{pmatrix} -17&13&-5\\0&-9&0\\6&10&-5\end{pmatrix}$

б)

$AB=\begin{pmatrix} 1&1&-1\\2&-4&1\\4&-3&1\end{pmatrix}*\begin{pmatrix} 1&0&-4\\2&5&-3\\4&-3&2\end{pmatrix}=\\\begin{pmatrix}1*1+1*2-1*4&1*0+1*5-1*(-3)&-4*1-3*1-1*2\\2*1-4*2+1*4&2*0-4*5-3*1&-4*2-4*(-3)+1*2\\4*1-3*2+1*4&4*0-3*5-3*1&-4*4-3*(-3)+1*2\end{pmatrix}=\\\begin{pmatrix} -1&8&-9\\-2&-23&6\\2&-18&-5\end{pmatrix}$

в) Перед поиском обратной матрицы проверим, существует ли она вообще. Поскольку обратные существуют только для невырожденных матриц, рассчитаем определитель и выясним, равен ли он нулю.

$\det A=\begin{vmatrix} 1&1&-1\\2&-4&1\\4&-3&1\end{vmatrix} =\begin{vmatrix} 1&1&-1\\0&-6&3\\4&-3&1\end{vmatrix} =\begin{vmatrix} 1&1&-1\\0&-6&3\\0&-7&5\end{vmatrix} =\\\begin{vmatrix} -6&3\\-7&5\end{vmatrix}=-6*5-(-7)*3=-30+21=-9 \ne 0$

Итак, A^-1 существует. Найдем ее. Для начала транспонируем A:

$A^T=\begin{pmatrix} 1&2&4\\1&-4&-3\\-1&1&1\end{pmatrix}$

Теперь заменим каждый элемент на его минор и умножим полученную матрицу на число, обратное определителю. Я опять-таки сделаю все подробно, но повторять не стоит:)

$A^{-1}=\frac{1}{\det A}\begin{pmatrix} -4*1-1*(-3)&-(1*1-(-1)*(-3))& 1*1-(-1)*(-4)\\-(2*1-1*4)& 1*1-(-1)*4&-(1*1-(-1)*2)\\-3*2-(-4)*4&-(-3*1-1*4)&-4*1-1*2\end{pmatrix} =\\-\frac{1}{9} \begin{pmatrix} -1&2&-3\\2&5&-3\\10&7&-6\end{pmatrix}=\frac{1}{9}\begin{pmatrix} 1&-2&3\\-2&-5&3\\-10&-7&6\end{pmatrix}$

Если мы сделали все правильно, то после умножения обратной матрицы на A (либо наоборот) получим единичную матрицу. Это как раз и предлагают провернуть в двух последних пунктах.

г)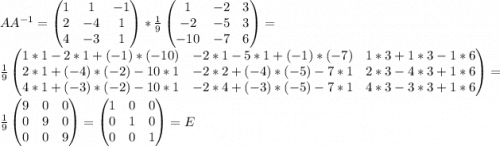 $AA^{-1}=\begin{pmatrix} 1&1&-1\\2&-4&1\\4&-3&1\end{pmatrix}*\frac{1}{9}\begin{pmatrix} 1&-2&3\\-2&-5&3\\-10&-7&6\end{pmatrix} =\\\frac{1}{9}\begin{pmatrix} 1*1-2*1+(-1)*(-10)&-2*1-5*1+(-1)*(-7)&1*3+1*3-1*6\\2*1+(-4)*(-2)-10*1&-2*2+(-4)*(-5)-7*1&2*3-4*3+1*6\\4*1+(-3)*(-2)-10*1&-2*4+(-3)*(-5)-7*1&4*3-3*3+1*6 \end{pmatrix}=\\\frac{1}{9}\begin{pmatrix} 9&0&0\\0&9&0\\0&0&9\end{pmatrix} =\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1\end{pmatrix}=E$ д) $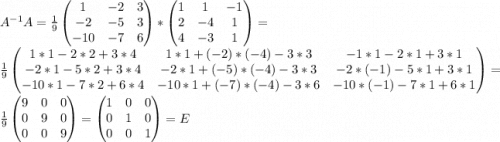A^{-1}A=\frac{1}{9} \begin{pmatrix} 1&-2&3\\-2&-5&3\\-10&-7&6\end{pmatrix}*\begin{pmatrix} 1&1&-1\\2&-4&1\\4&-3&1\end{pmatrix}=\\\frac{1}{9}\begin{pmatrix} 1*1-2*2+3*4&1*1+(-2)*(-4)-3*3&-1*1-2*1+3*1\\-2*1-5*2+3*4&-2*1+(-5)*(-4)-3*3&-2*(-1)-5*1+3*1\\-10*1-7*2+6*4&-10*1+(-7)*(-4)-3*6&-10*(-1)-7*1+6*1\end{pmatrix} =\\\frac{1}{9}\begin{pmatrix} 9&0&0\\0&9&0\\0&0&9\end{pmatrix} =\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1\end{pmatrix}=E$

0,0(0 оценок)

Ответ:

дэдшотер

16.12.2021 15:29

(x-1,25) / -3 = y / 4 = (z-0,25) / 5

Пошаговое объяснение:

$L:\begin{cases} 2x-y+2z-3=0 \; \; \; (P_1)\\ x+2y-z-1=0 \; \; \; \; \; (P_2)\end{cases} (*)$

Для построения канонического уравнения прямой необходимо и достаточно знать ее направляющий вектор q и какую угодно точку на этой прямой. Искомая прямая L задана как пересечение плоскостей P_1 и P_2, то есть она лежит в обеих плоскостях. Тогда нормальные векторы каждой плоскости, будучи перпендикулярны к "своим" плоскостям, будут перпендикулярны и к любой прямой, лежащей в "своей" плоскости, в том числе и к L. Другими словами, L перпендикулярна нормальному вектору как P_1, так и P_2. А значит, ее направляющий вектор является векторным произведением нормальных векторов P_1 и P_2

Координаты нормального вектора плоскости — коэффициенты при x, y и z в общем уравнении этой плоскости:

$\vec{n_1}=(2;-1;2)\\\vec{n_2}=(1;2;-1)$

Их векторное произведение найдем, вычислив определитель:

$[\vec{n_1}, \vec{n_2}]=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k}\\2&-1&2\\1&2&-1\end{vmatrix}=\vec{i}\begin{vmatrix} -1&2\\2&-1\end{vmatrix}-\vec{j}\begin{vmatrix} 2&2\\1&-1\end{vmatrix}+\vec{k}\begin{vmatrix} 2&-1\\1&2\end{vmatrix}=\\(-1*(-1)-2*2)\vec{i}-(2*(-1)-1*2)\vec{j}+(2*2-1*(-1))\vec{k}=\\(1-4)\vec{i}-(-2-2)\vec{j}+(4+1)\vec{k}=-3\vec{i}+4\vec{j}+5\vec{k}=(-3;4;5)=\vec{q}$

В качестве точки на L возьмем частное решение системы (*). Пускай y = 0, тогда

$\begin{cases}2x+2z-3=0 \\x-z-1=0 \; | \; *2 \end{cases}\\ \begin{cases}2x+2z-3=0\\2x-2z-2=0 \end{cases} \bigg| \; +\\ \begin{cases} 4x-5=0, \; x=\frac{5}{4} \\z=x-1=\frac{5}{4}-1=\frac{1}{4} \end{cases}$