Дано: Скорость поезда 60 км/ч;
время отправления 7 ч утра;
скорость самолета 660 км/ч;
время вылета 13 ч след.дня.
Вопрос: Через сколько часов самолет догонит поезд?
Решение: 1) 24 - 7 = 17 (ч) столько часов поезд был в пути в первые сутки;
2) 17 + 13 = 30 (ч) столько часов поезд был в пути всего;
3) 60 * 30 = 1800 (км) такое расстояние проехал поезд за 30 ч;
4) 660 - 60 = 600 (км/ч) разница скоростей самолета и поезда;
5) 1800 : 600 = 3 (ч) через столько времени самолет догонит поезд.
ответ: через 3 часа после вылета, т. е. в 16.00.
x1 = 8 м/с и x2 = 10 м/с - в момент времени t1 = 1
x1 = 24 м/с и x2 = 22 м/с в момент времени t2 = 3
Пошаговое объяснение:
Указанные законы
описывают функциональные зависимости расстояния х1 и х2 от времент t
Моментами, когда пройденные точками расстояния равны, будут такие моменты времени t, при которых
будет соблюдаться равенство:
Скорости точек v1 ,v2 определяются как производные от функций расстояния в заданные моменты времени t,
1. Определим моменты времени t, когда выполняется равенство
Решим уравнение
По Т. Виета разбиваем на множители:
2. Найдем скорости точек в моменты времени t1 и t2
2а) Определим формулы скорости:
2б) Найдем скорости точек в моменты времени t1 и t2
Дано: Скорость поезда 60 км/ч;
время отправления 7 ч утра;
скорость самолета 660 км/ч;
время вылета 13 ч след.дня.
Вопрос: Через сколько часов самолет догонит поезд?
Решение: 1) 24 - 7 = 17 (ч) столько часов поезд был в пути в первые сутки;
2) 17 + 13 = 30 (ч) столько часов поезд был в пути всего;
3) 60 * 30 = 1800 (км) такое расстояние проехал поезд за 30 ч;
4) 660 - 60 = 600 (км/ч) разница скоростей самолета и поезда;
5) 1800 : 600 = 3 (ч) через столько времени самолет догонит поезд.
ответ: через 3 часа после вылета, т. е. в 16.00.
x1 = 8 м/с и x2 = 10 м/с - в момент времени t1 = 1
x1 = 24 м/с и x2 = 22 м/с в момент времени t2 = 3
Пошаговое объяснение:
Указанные законы
описывают функциональные зависимости расстояния х1 и х2 от времент t
Моментами, когда пройденные точками расстояния равны, будут такие моменты времени t, при которых
будет соблюдаться равенство:
Скорости точек v1 ,v2 определяются как производные от функций расстояния в заданные моменты времени t,
1. Определим моменты времени t, когда выполняется равенство
Решим уравнение
По Т. Виета разбиваем на множители:
2. Найдем скорости точек в моменты времени t1 и t2
2а) Определим формулы скорости:
2б) Найдем скорости точек в моменты времени t1 и t2
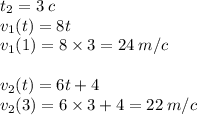
8 м/с и 10 м/с в момент времени t1 = 124 м/с и 22 м/с в момент времени t2 = 3