Температурасы неше радус
618. хауи
бола
3. әлияның ойлаған санын 6-ға бөліп, бөліндіге 2
санын үстана
өзге
не
қосынды -5,25-ке тең болды. әлия кандай сан ойлады?
в
619. а​

Пошаговое объяснение:

1.1 Прочертим диагональ и получим треугольник со сторонами 8,3 и углом между ними 120°

По теореме косинусов можем вычислить диагональ(третью сторону)

a²=b²+c²-2bc*cos120

a²=64+9-2*8*3*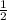

a²=49

a=7

Диагональ равна 7

1.2 Sпараллелограмма=h*a

Проведем высоту к сторону равной 8

угол между высотой и меньшей стороной будет 120-90=30, а значит мы получаем прямоугольный треугольник с углом в 30° и гипотенузой равной 3

Следовательно сторона напротив угла в 30°=3/2=1,5

По теореме Пифагора находим высоту

9=h²+2,25

h=2,5

Sпараллелограмма=2,5*8=20

2. Тут понадобится теорема синусов

(8√2)/(sin45)=(8√3)/(sinx)

sin45=√2/2

(8√2)/(√2/2)=16 ⇒ (8√3)/(sinx)=16

sinx=(8√3)/16=√3/2

sinx=√3/2 ⇒ x=60°

∠D=60°

3. Sсектора=(πR²*α)/(360)

В правильном шестиугольнике a=R⇒R=6

α=60

Sсектора=(36*60π)/(360)

Sсектора=6π≈18,84

4. АВ=√18

BC=√((-1-(-5))²+(-5-(-1))²)=√32

СD=√18

AD=√((2-(-2)²+(-2-2)²)=√32

Из этих вычислений следует то, что ABCD параллелограмм

Если AC²=AB²+BC²=AD²+CD² ,то ABCD прямоугольник

AC=√50

(√50)²=(√18)²+(√32)²

50=18+32⇒ABCD прямоугольник

5. Уравнение окружности это

(x-xцентра)²+(y-yцентра)²=R²

(x+7)²+(y-1)²=81

Центр окружности в точке (-7;1); R=9

При параллельном переносе на  {3;-8} центр окажется в точке (-4;-7); радиус не изменится, значит уравнение будет выглядить вот так

(x+4)²+(y+7)²=81

Пусть лягушонок стартует в точке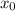 . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке 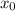дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение 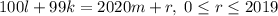имеет решение при любом , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку ;

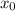Докажем для начала, что если существует решение для остатков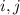 , то существует решение для остатка 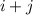. Это вполне очевидно: просто сложим два уравнения для остатков 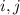. Теперь, в частности, если существует решение для 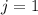, то существует решение для всех остатков. То есть нам надо решить диофантово уравнение 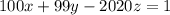; Для этого сразу положим 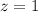; Пусть ;

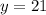Тогда из числа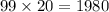 нам нужно получить число 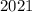; Но мы умеем прибавлять единицу: 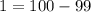. То есть 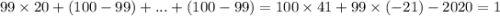; Иными словами, получили решение 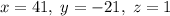, но нам нужно решение в натуральных числах. Не вопрос: добавим к 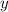2020, а к добавим 99. Получим решение: .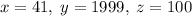

Итак, план действий следующий.

Пусть мы находимся в точке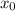 . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке 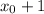. Таким образом, мы посетим все точки.