Теория вероятности только ответ шагов не надо Дано множество Rn = {1, 2, ... , п}. Производится п испытаний Бернулли с вероятностью успеха р. Если в 2-ом испытании успех, то элемент 1 кладется в строящееся случайное множество А1. Иначе не кладется. В итоге образуется А1 С Кп. Аналогично (как бы забыв про А1) можно построить множество А2. Таким образом строится т случайных множеств A1, Атс Р Н. Найдите вероятность того, что
Решение. Убедимся, что точка не лежит на прямой, данной в условии:
4/5 ≠ (3-1)/-1 ≠ (1+3)/3.
Из уравнения данной прямой следует, что точка M1(0;1; -3) лежит на этой прямой.
Пусть M(x;y;z) - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4) и s(5; -1; 3) компланарны. Следовательно, их смешанное произведение равно нулю:
1) Т.к. ABCD - параллелограмм, то его противолежащие стороны параллельны и равны, т.е. АВ||EF, AB=EF, АE||BF, AE=BF.
2) Т.к. DCEF - параллелограмм, то его противолежащие стороны параллельны и равны, т.е. DC||EF, DC=EF, DE||CF, DE=CF.
3) По доказанному выше AB||EF||DC и AB=EF=DC ⇒ по признаку (равенство и параллельность одной пары противолежащих сторон четырехугольника) ABCD является параллелограммом.
4) По свойству диагоналей параллелограмма ABCD имеем: AE=EC и DE=EB. ⇒ EC=AE=BF и EB=DE=CF. Отсюда по признаку (равенство пар противолежащих сторон четырехугольника) EBFC является параллелограммом.
Провести плоскость через прямую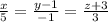
и точку Mo(4; 3; 1).
Решение. Убедимся, что точка не лежит на прямой, данной в условии:
4/5 ≠ (3-1)/-1 ≠ (1+3)/3.
Из уравнения данной прямой следует, что точка M1(0;1; -3) лежит на этой прямой.
Пусть M(x;y;z) - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4) и s(5; -1; 3) компланарны. Следовательно, их смешанное произведение равно нулю:
x-4 y-3 z-1| x-4 y-3
4 2 4| 4 2
5 -1 3| 5 -1 =
= 6(x-4) + 20(y-3) - 4(z-1) - 12(y-3) + 4(x-4) - 10(z-1) =
= 6x -24 +20y - 60 - 4z + 4 - 12y + 36 + 4x - 16 - 10z + 10 =
= 10x + 8y - 14z - 50 = 0 или, сократив на 2:
5x + 4y - 7z - 25 = 0.
Таким образом, нормальный вектор искомой плоскости равен:
(5; 4; -7).
Чертеж беру ваш.
1) Т.к. ABCD - параллелограмм, то его противолежащие стороны параллельны и равны, т.е. АВ||EF, AB=EF, АE||BF, AE=BF.
2) Т.к. DCEF - параллелограмм, то его противолежащие стороны параллельны и равны, т.е. DC||EF, DC=EF, DE||CF, DE=CF.
3) По доказанному выше AB||EF||DC и AB=EF=DC ⇒ по признаку (равенство и параллельность одной пары противолежащих сторон четырехугольника) ABCD является параллелограммом.
4) По свойству диагоналей параллелограмма ABCD имеем: AE=EC и DE=EB. ⇒ EC=AE=BF и EB=DE=CF. Отсюда по признаку (равенство пар противолежащих сторон четырехугольника) EBFC является параллелограммом.
Доказано.