Точки A, B, C, D, E, F, M и K разделили окружность на 8 разных дуг. Найдите градусные меры указанных углов. 1)угол ABK=
2)угол ACK=
3)угол ADM=
4)угол AFM=
5)угол AMF=
6) угол BDF=​

Из треугольника АВС найдем \angle ABC:
\angle ABC=180 в степени circ минус \angle A минус \angle C=180 в степени circ минус 40 в степени circ минус 60 в степени circ=80 в степени circ.
BD — биссектриса, следовательно, \angle DBC= дробь, числитель — 1, знаменатель — 2 \angle ABC=40 в степени circ.
Треугольник HBC — прямоугольный, следовательно:
\angle HBC=90 в степени circ минус \angle C=90 в степени circ минус 60 в степени circ=30 в степени circ.
Найдём угол DBH:
\angle DBH=\angle DBC минус \angle HBC=40 в степени circ минус 30 в степени circ=10 в степени circ.

ответ: 10°.

A

Пошаговое объяснение:

Первое, что стоит заметить - область определения функции: .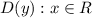

Функция будет убывать на всей числовой оси (т.е., монотонно убывающей) тогда и только тогда, когда её производная будет неположительной:

.

График функции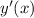  - парабола, причём направлена ветками вниз (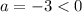), а поэтому её область значений всегда будет неположительной, если она не имеет точек пересечения с осью абсцисс или касается её. Отсюда вытекает, что квадратное уравнение не имеет решений или имеет только одно только при .

.

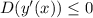Отсюда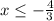 .