треугольник mnk - равнобедренный
a принадлежит mn
b принадлежит kn
ma=kb
докажите что угол bmk= углу akm

Я докажу первое и последнее, остальное - сам.

1)

Доказательство "⇒".

Пусть у нас дано ((A∪B)⊂C), докажем тогда, что

1.1) A⊂C,

и

1.2) B⊂C.

1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.

1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.

чтд.

Доказательство "<=".

Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что

A∪B⊂C.

Пусть x∈A∪B, ⇔ x∈A или x∈B.

a) x∈A⊂C, ⇒ x∈C.

б) x∈B⊂C, ⇒ x∈C.

То есть A∪B⊂C.

чтд.

4)

Доказательство "⇒".

Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что

Пусть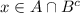 , ⇔ 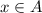и , ⇔

и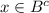

Тогда т.к. A⊂B∪C, имеем

и

Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.

Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.

чтд.

Доказательство "<=".

Пусть у нас дано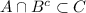 , докажем тогда, что

A⊂ B∪C.

Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.

Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.

Случай второй: x∈A и x∉B, ⇒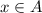 и , ⇒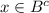

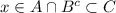⇒ , ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.

чтд.

Верные утверждения:
1) В любой треугольник можно вписать окружность.

5) Любые два равносторонних треугольника подобны.  
По первому признаку подобия треугольников - любые равносторонние треугольники будут подобны, т.к. 2 угла одного треугольника равны 2-ум углам другого (по 60°)

НЕ ВЕРНЫЕ УТВЕРЖДЕНИЯ:
2) Любые два прямоугольных треугольника подобны.
НЕТ, необходимо, чтобы 2 угла были равны, по первому признаку подобия треугольников. 

3) Центр описанной около треугольника окружности лежит в точке пересечения биссектрис углов треугольника.
НЕт, центр - это точка пересечения серединных перпендикуляров к сторонам треугольника

4) Площадь трапеции равна сумме оснований, умноженной на высоту.
НЕТ, площадь трапеции - это ПОЛУСУММА оснований умноженная на высоту.