У трапеції АВСD відомо, що АВ = CD = 17см, AD = 32см. Через центр О кола, вписаного в цю трапецію, проведено перпендикуляр PO до площини трапеції, PO = корінь 65см. Знайдіть відстань від точки P до сторін трапеції.
Покажем, что никакие 2 числа из не могут давать одинаковые остатки от деления на n.
Пусть не так, и .
Но тогда их разность делится на n. Отсюда следует, с учетом взаимной простоты n и d, что делится на n. Но, нетрудно заметить, - противоречие.
Значит, числа дают различные остатки при делении на n. Но этих чисел ровно n - значит, среди них обязательно найдется число, дающее остаток 0 при делении на n. Противоречие с тем, что числа взаимно простые с n.
Это и означает, что числа n и d не взаимно простые.
НОД
Разложим на простые множители 14
14 = 2 • 7
Разложим на простые множители 35
35 = 5 • 7
Выберем одинаковые простые множители в обоих числах.
7
Находим произведение одинаковых простых множителей и записываем ответ
НОД (14; 35) = 7 = 7
НОК
Разложим на простые множители 14
14 = 2 • 7
Разложим на простые множители 35
35 = 5 • 7
Выберем в разложении меньшего числа (14) множители, которые не вошли в разложение
2
Добавим эти множители в разложение бóльшего числа
5 , 7 , 2
Полученное произведение запишем в ответ.
НОК (14, 35) = 5 • 7 • 2 = 70
ответ: В 10 раз
Пусть не так, и и числа n и d взаимно простые.
Покажем, что никакие 2 числа из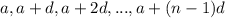
не могут давать одинаковые остатки от деления на n.
Пусть не так, и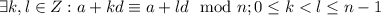
.
Но тогда их разность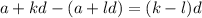
делится на n. Отсюда следует, с учетом взаимной простоты n и d, что 
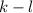делится на n. Но, нетрудно заметить, 
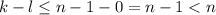- противоречие.
Значит, числа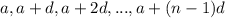
дают различные остатки при делении на n. Но этих чисел ровно n - значит, среди них обязательно найдется число, дающее остаток 0 при делении на n. Противоречие с тем, что числа 
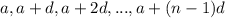взаимно простые с n.
Это и означает, что числа n и d не взаимно простые.
Ч.т.д.