1. найдем производную. 6х²-12х-18=6*(х²-2х-3), найдем критические точки. 6*(х²-2х-3)=0, по Виету х=-1; х=3
-13
+ - +
функция возрастает при х∈(-∞;-1] и при х∈ [3;+∞), и убывает при х∈ [-1;3]
2 производная равна 6х²-6х-12=0; 6(х²-х-2)=0; по Виету х=2; х=-1
-12
функция возрастает при х∈(-∞;-1] и при х∈ [2;+∞), и убывает при х∈ [-1;2]
3.производная равна -4/х²+2/х³=(2-4х)/х³; х=0; х=0.5
00.5
- + -
х=0.5- точка максимума, максимум равен 4/(1/2)-1/(1/2)²=8-4=4
4. производная равна -10/х²+14/х³=0, 14-10х=0; х=1.4
01.4
х=х=1.4- точка максимума, максимум равен 10/(1.4)-1/(1.4)²=1300/196=
315/49
Область определения: x - любое число.
Четность: функция нечетная.
Пошаговое объяснение:
1) Знаменатель больше нуля при любых значениях независимой переменной x, так как это сумма двух положительных чисел.
Значит при любых значениях x знаменатель не равен нулю:
x² + 1 ≠ 0
Операции вычитания и умножения определены для любых чисел. ⇒
Областью допустимых значений функции является любое число.
2) Чтобы определить четность функции, найдем значение y(-x):
Функция является нечетной, так как для любого значения x из области определения выполняется условие y(-x) = - y(x).
1. найдем производную. 6х²-12х-18=6*(х²-2х-3), найдем критические точки. 6*(х²-2х-3)=0, по Виету х=-1; х=3
-13
+ - +
функция возрастает при х∈(-∞;-1] и при х∈ [3;+∞), и убывает при х∈ [-1;3]
2 производная равна 6х²-6х-12=0; 6(х²-х-2)=0; по Виету х=2; х=-1
-12
+ - +
функция возрастает при х∈(-∞;-1] и при х∈ [2;+∞), и убывает при х∈ [-1;2]
3.производная равна -4/х²+2/х³=(2-4х)/х³; х=0; х=0.5
00.5
- + -
х=0.5- точка максимума, максимум равен 4/(1/2)-1/(1/2)²=8-4=4
4. производная равна -10/х²+14/х³=0, 14-10х=0; х=1.4
01.4
- + -
х=х=1.4- точка максимума, максимум равен 10/(1.4)-1/(1.4)²=1300/196=
315/49
Область определения: x - любое число.
Четность: функция нечетная.
Пошаговое объяснение:
1) Знаменатель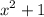
больше нуля при любых значениях независимой переменной x, так как это сумма двух положительных чисел.
Значит при любых значениях x знаменатель не равен нулю:
x² + 1 ≠ 0
Операции вычитания и умножения определены для любых чисел. ⇒
Областью допустимых значений функции является любое число.
2) Чтобы определить четность функции, найдем значение y(-x):
Функция является нечетной, так как для любого значения x из области определения выполняется условие y(-x) = - y(x).