Выделим из [0;1] счетное множество и обозначим . При этом, нетрудно заметить, .
Тогда построим отображение отрезка [0;1] на интервал (0;1]:
Т.е. каждый из членов последовательности "превращается" в следующий за ним, а все остальные значения аргумента остаются неизменными. Как видим, каждому элементу отрезка соответствует ровно один элемент интервала, и наоборот. Это и означает, что построенное отображение является взаимно-однозначным (но не единственным, в силу неоднозначности задания ).
Выделим из [0;1] счетное множество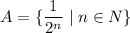 и обозначим
и обозначим 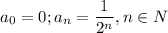 . При этом, нетрудно заметить,
. При этом, нетрудно заметить, 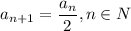 .
.
Тогда построим отображение отрезка [0;1] на интервал (0;1]:
Т.е. каждый из членов последовательности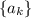 "превращается" в следующий за ним, а все остальные значения аргумента остаются неизменными.
"превращается" в следующий за ним, а все остальные значения аргумента остаются неизменными. 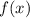 ).
).
Как видим, каждому элементу отрезка соответствует ровно один элемент интервала, и наоборот. Это и означает, что построенное отображение является взаимно-однозначным (но не единственным, в силу неоднозначности задания