Пусть Олег "сократил" дробь x раз. Тогда, по условию, Аня "сократила" дробь 30-x раз. Тогда Олег отнимает от знаменателя 2019 число 3·x, а Аня число 2·(30-x), то есть отняли число 3·x+2·(30-x). В итоге они получили 1952. Тогда Олег и Аня отняли от знаменателя:
2019 - 1952 = 67.
Поэтому
3·x+2·(30-x)=67
3·x+60-2·x=67
x=67-60=7.
Значит, Олег отнял 7 раз, а Аня отняла 30-7=23.
Тогда Олег отнял от числителя 7 раз 4, а Аня отняла от числителя 23 раза 3. Отсюда, числитель дроби равна
где — абсцисса точки графика функции , к которому проведена касательная .
Так как график касательной имеет вид график прямой линейной функции , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
Таким образом, касательная будет горизонтальной, если
Найдем :
Найдем :
Следовательно, — абсцисса точки графика функции , к которому проведена касательная .
Найдем значение :
Таким образом, — уравнение горизонтальной касательной к графику функции
1921
Пошаговое объяснение:
Пусть Олег "сократил" дробь x раз. Тогда, по условию, Аня "сократила" дробь 30-x раз. Тогда Олег отнимает от знаменателя 2019 число 3·x, а Аня число 2·(30-x), то есть отняли число 3·x+2·(30-x). В итоге они получили 1952. Тогда Олег и Аня отняли от знаменателя:
2019 - 1952 = 67.
Поэтому
3·x+2·(30-x)=67
3·x+60-2·x=67
x=67-60=7.
Значит, Олег отнял 7 раз, а Аня отняла 30-7=23.
Тогда Олег отнял от числителя 7 раз 4, а Аня отняла от числителя 23 раза 3. Отсюда, числитель дроби равна
2018-4·7-3·23=2018-28-69=1921.
Уравнение касательной имеет вид:
где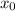
— абсцисса точки графика функции 
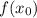, к которому проведена касательная 
.
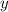Так как график касательной имеет вид график прямой линейной функции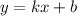
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —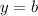 
Таким образом, касательная будет горизонтальной, если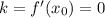
Найдем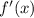
:
Найдем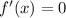
:
Следовательно,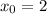
— абсцисса точки графика функции 
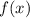, к которому проведена касательная 
.
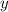Найдем значение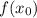
:
Таким образом,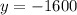
— уравнение горизонтальной касательной к графику функции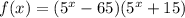 
ответ: