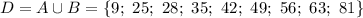В футбольном турнире участвует несколько команд, при этом к данному моменту каждая команда сыграла ровно 20 игр. Оказалось, что у каждой команды не более 8 побед и не менее 8 поражений. Сколько очков может иметь к данному моменту команда-лидер? Лидеров может быть несколько. За победу дается 3 очка, за ничью – 1 очко, за поражение – 0 очков. (ответ+обоснование, указать все вариан-ты)
Свойства степеней(≈7 класс):
Упростите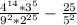
Квадратное уравнение(≈8 класс):
x² – 46x + 529 = 0
С использованием производной(≈11 класс):
y(x) = x⁴ + x³ - 5x² - x + 17
y'(2) = ?
↓↓↓↓↓
Свойства степеней(решение):
Квадратное уравнение(решение):
x² – 46x + 529 = 0
D = b² - 4ac = (-46)² - 4 * 1 * 529 = 2116 - 2116 = 0 => один корень
x = -b/2a = -(-46)/2 = 46/2 = 23
С использованием производной(решение):
y(x) = x⁴ + x³ - 5x² - x + 17
y'(2) = ?
y'(x) = (x⁴)' + (x³)' - (5x²)' - (x)' + (17)' = 4x³ + 3x² - 10x - 1
y'(2) = 4*2³ + 3*2² - 10*2 - 1 = 4*8 + 3*4 - 20 - 1 = 32 + 12 - 21 = 44 - 21 = 23
Составим множество А. Выпишем нечётные натуральные числа из отрезка от 3 до 9:
3; 5; 7; 9
Теперь возведем их в квадрат:
9; 25; 49; 81
Значит:
Составим множество В. Выпишем целые числа из интервала от 3 до 10:
4; 5; 6; 7; 8; 9
Умножим их на 7:
28; 35; 42; 49; 56; 63
Значит:
Находим пересечение множеств А и В. В пересечение попадают элементы, принадлежащие одновременно и множеству А и множеству В:
Находим объединение множеств А и В. В объединение попадают элементы, принадлежащие хотя бы одному из множеств А или В: