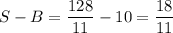Упорядочим числа по возрастанию (a₁ < a₂ < ... < a₁₁). Тогда по условию:
а) Если a₁ = 5, то a₂ ≥ 6, a₃ ≥ 7, ... a₆ ≥ 10. Тогда a₁ + a₂ + ... + a₆ ≥ 5 + 6 + ... + 10 = 45, но сумма шести наименьших чисел равна 42, она не может быть больше или равна 45. Значит, такое невозможно.
б) Если такое возможно, то
Сложим уравнения (1) и (2): a₁ + a₂ + ... + a₅ + 2a₆ + a₇ + ... + a₁₁ = 138. Но мы знаем, что a₁ + a₂ + ... + a₅ + a₆ + a₇ + ... + a₁₁ = 110. Тогда 110 + a₆ = 138 ⇔ a₆ = 28 ⇒ a₇ ≥ 29, a₈ ≥ 30, ... , a₁₁ ≥ 33 ⇒ a₆ + a₇ + ... + a₁₁ ≥ 28 + 29 + ... + 33 = 183. Минимально возможная сумма шести наибольших чисел в таком случае равна 183, что больше 96. Значит, такое невозможно.
в) Проведём действия, аналогичные пункту б):
a₁ + a₂ + ... + a₅ + 2B + a₇ + ... + a₁₁ = 138 ⇒ 11S + B = 138 ⇔ ⇒ . Данное выражение максимально при минимальном значении B.
Если a₆ = B, то в силу различности написанных чисел a₅ ≤ B - 1, a₄ ≤ B - 2, ... , a₁ ≤ B - 5. Тогда 42 = a₁ + a₂ + ... a₆ ≤ 6B - 15 ⇒ 6B ≥ 57 ⇔ B ≥ 9,5 ⇒ B ≥ 10. Тогда
Действительно, такое значение достигается, например, если были выписаны числа 2, 6, 7, 8, 9, 10, 11, 12, 13, 14, 36. Среднее арифметическое шести наименьших равно , среднее арифметическое шести наибольших равно , среднее арифметическое всех чисел ,
S полн.= S осн + S бок
S осн = √(р·(р-а)(p-b)(p-c)) ,где р - полупериметр:
р= (a+ b+ c)/2 = (10+10+12)/2 = 16, тогда
S осн = √(р·(р-а)(p-b)(p-c))= √(16·6·6·4) =4·6·2= 48 ( см²).
2) Если боковые грани наклонены к плоскости основания под одним углом,
то площадь боковой поверхности равна половине произведения периметра
основания на высоту боковой грани: S бок = P осн·SH = 32·SH =...
Если боковые грани наклонены к плоскости основания под одним углом, то
в основание пирамиды можно вписать окружность, причём вершина пирамиды
проецируется в её центр, т.е. НО = r = Sосн/ p=48/16= 3 (см)
Из ΔSOH - прям.: L SHO = 45⁰, тогда L SHO = 45⁰, значит ΔSHO - равнобедрен.
и SO=ОН=3 см, SH = 3√2 см .
S бок = P осн·SH = 32·SH = 32·3√2 = 96√2 (см²)
Таким образом S полн = 48 + 96√2 = 48(1+ 2√2) (см²).
а) нет
б) нет
в) 18 / 11
Пошаговое объяснение:
Упорядочим числа по возрастанию (a₁ < a₂ < ... < a₁₁). Тогда по условию:
а) Если a₁ = 5, то a₂ ≥ 6, a₃ ≥ 7, ... a₆ ≥ 10. Тогда a₁ + a₂ + ... + a₆ ≥ 5 + 6 + ... + 10 = 45, но сумма шести наименьших чисел равна 42, она не может быть больше или равна 45. Значит, такое невозможно.
б) Если такое возможно, то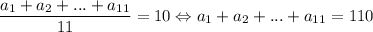
Сложим уравнения (1) и (2): a₁ + a₂ + ... + a₅ + 2a₆ + a₇ + ... + a₁₁ = 138. Но мы знаем, что a₁ + a₂ + ... + a₅ + a₆ + a₇ + ... + a₁₁ = 110. Тогда 110 + a₆ = 138 ⇔ a₆ = 28 ⇒ a₇ ≥ 29, a₈ ≥ 30, ... , a₁₁ ≥ 33 ⇒ a₆ + a₇ + ... + a₁₁ ≥ 28 + 29 + ... + 33 = 183. Минимально возможная сумма шести наибольших чисел в таком случае равна 183, что больше 96. Значит, такое невозможно.
в) Проведём действия, аналогичные пункту б):
a₁ + a₂ + ... + a₅ + 2B + a₇ + ... + a₁₁ = 138 ⇒ 11S + B = 138 ⇔
⇒ 
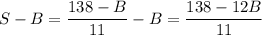. Данное выражение максимально при минимальном значении B.
Если a₆ = B, то в силу различности написанных чисел a₅ ≤ B - 1, a₄ ≤ B - 2, ... , a₁ ≤ B - 5. Тогда 42 = a₁ + a₂ + ... a₆ ≤ 6B - 15 ⇒ 6B ≥ 57 ⇔ B ≥ 9,5 ⇒ B ≥ 10. Тогда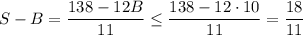
Действительно, такое значение достигается, например, если были выписаны числа 2, 6, 7, 8, 9, 10, 11, 12, 13, 14, 36. Среднее арифметическое шести наименьших равно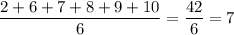
, среднее арифметическое шести наибольших равно 
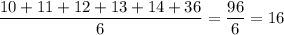, среднее арифметическое всех чисел 
, 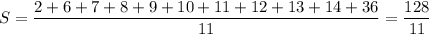