В прямоугольной трапеции ABCD с основаниями AD и BC диагональ BD равна 32, а угол А равен 45°. Найдите большую боковую сторону, если меньшее основание трапеции
равно 85.

Показать ответ

Ответ:

VETALmc005

24.08.2020 05:31

Гипотенуза прямоугольного треугольника в 2 раза больше медианы, проведённой к ней. Это следует из того, что центр окружности, описанной около прямоугольного треугольника, лежит в середине его гипотенузы. Следовательно AB=5 см.

Один из катетов меньше гипотенузы на 1, следовательно, он равен 4 см. Оставшийся катет можно найти по теореме Пифагора или вспомнить, что данный треугольник является египетским. Оставшийся катет равен 3 см. Периметр треугольника равен 3+4+5=12 (см) .

ответ. 12 см

Пошаговое объяснение:

0,0(0 оценок)

Ответ:

sofyaoborina12

21.03.2023 21:16

Пусть первый спортсмен вернулся к месту старта через x минут после начала своего заплыва. x мин = 60x секунд.

Значит, от одного другого конца бассейна первый доплывает за 60x:2 = 30x секунд.

Пусть длина дорожки y метров (можно и за единицу принять - всё равно сократится потом).

Тогда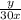 $\frac y{30x}$ м/с скорость первого пловца, 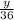$\frac y{36}$ м/с - скорость второго.

От конца дорожки до места встречи первый доплыл за 30x-25 секунд. Второй от начала дорожки до места встречи доплыл за то же время, т.к. начали встречное движение одновременно.

За это время первый проплыл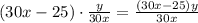 $(30x-25)\cdot\frac y{30x}=\frac{(30x-25)y}{30x}$ метров, второй 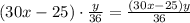$(30x-25)\cdot\frac y{36}=\frac{(30x-25)y}{36}$ метров. В сумме проплыли расстояние, равное длине дорожки, то есть

$\frac{(30x-25)\not y}{30x}+\frac{(30x-25)\not y}{36}=\not y\\\\\frac{30x-25}{30x}+\frac{30x-25}{36}=1\\\\\frac{(30x-25)\cdot6+(30x-25)\cdot5x}{180x}=1\\\\\frac{(30x-25)(5x+6)}{180x}=1\\\\150x^2+180x-125x-150=180x\\150x^2-125x-150=0\;\;\;\div25\\6x^2-5x-6=0\\D=25-4\cdot6\cdot(-6)=25+144=169=(\pm13)^2\\x_{1,2}=\frac{5\pm13}{12}\\x_1=-\frac8{12}=-\frac34\;-\;He\;nogx\\x_2=\frac{18}{12}=1,5$