В6. Найдите сумму абсцисс точек пересечения (или абсциссу, если точка одна) графика функции y = 4log: 1-х) с прямой, параллельной оси абсцисс и проходящей через точку (-2; 25).
Многочлены третьей и четвёртой степеней можно разложить на множители, если множители свободного члена являются корнями уравнения, в котором многочлен приравнивается нулю.
В нашем случае такие данные:
1 -1 2 -2 3 -3 4 -4 6 -6
20 0 0 32 -48 180 -100 540 0 2400.
Как видим, три множителя соответствуют корням.
Это х1= -1, х2 = 2, х3 = 6.
Далее надо делить многочлен на двучлен с одним из полученных значений. Например так:
Если все числа правильно записаны, то ответ получается вот такой ( смотри ниже. Но смущают не целые числа, хотя всё остальное правильно)
Пошаговое объяснение:
Пусть во 2 день продали на х сум, тогда по условию в 1 день ( х + 23500) сум, а в 3 день ( х + 23500 - 56000) = ( х - 32500). Всего продано на
1 971 500 сум. Составим и решим уравнение:
( х + 23500) + х + ( х - 32500) = 1 971 500
3х - 9000 = 1 971 500
3х = 1 971 500 + 9000
3х = 1 980 500
х= 1 980 500 : 3
х = 660 166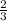
Значит, во второй день было продано на 660 166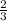
сум, тогда в первый день на 683 666
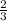сум, а в трети1 день 627 666
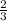сум.
Многочлены третьей и четвёртой степеней можно разложить на множители, если множители свободного члена являются корнями уравнения, в котором многочлен приравнивается нулю.
В нашем случае такие данные:
1 -1 2 -2 3 -3 4 -4 6 -6
20 0 0 32 -48 180 -100 540 0 2400.
Как видим, три множителя соответствуют корням.
Это х1= -1, х2 = 2, х3 = 6.
Далее надо делить многочлен на двучлен с одним из полученных значений. Например так:
x⁴-6x³-3x²+16x+12| (x + 1)
x⁴+x³ x³-7x²+4x+12
-7x³-3x²
-7x³-7x²
4x²+16x
4x²+4x
12x+12
12x+12
0
ответ: x⁴-6x³-3x²+16x+12 = (x-6)(x-2)(x+1)².