1. Что бы сложить дроби с разными знаменателямми надо сначала привести их к наименьшему общему знаменателю, а затем складывать их как дроби с одинаковыми знаменателями.
2. есть два варианта: ▪1-ый - это перевести смешанные числа в неправильную дробь и склмдывать их как дроби. ▪2-ой вариант - это надо сначала сложить целую часть, потом складываем дробную часть и после этого складываем полученные результаты при сложении целой и дробной частей
3. Что бы найти дробь от числа надо число умножить на эту дробь, т.е.
4. при умножении дробей надо перемножить числители и знаменатели этих дробей, т.е. умножение дроби на дробь дает дробь, числитель которой равен произведение числителей умножаемых дробей, а знаменатель равен произведению знаменателей умножаемых дробей 5. при умножении смешанных чисел сначала переводим их в неправильную дробь, а затем умножаем как дроби в п.4.
6. ----
7. что бы разделить дробь a/b на c/d надо делимое ( a/b ) умножить на число обратное делителю (d/c). 8. при деление смешанных чисел надо сначала их перевести в неправильную дробь а затем делить как в п.7
Тут, скорее, подойдёт метод пристального взгляда, с которого можно подобрать какие-то решения (это я к тому, чтобы не спрашивали, откуда взялись именно такие решения, всё методом проб и ошибок). Возьмём b = 2018k, d = ab, c ⋮ a, c / a = m. Тогда в первом уравнении получится . Во втором уравнении получаем . Чтобы легче было считать, возьмём k квадратом какого-нибудь числа. Если k = 1, то b = 2018, c = 2017 * 2019, a = 2017 или 2019. Уже отсюда видим, что a + m = 2017 + 2019 > 2018. Возьмём k = 4: b = 8072, c = 4035 * 4037, a = 4037 (оставим это), d = 4037 * 8072. Тогда для первого уравнения - верно. Для второго: - верно. Таким образом, четвёрка a = 4037, b = 8072, c = 4035 * 4037, d = 4037 * 8072 нам подходит.
2. есть два варианта:
▪1-ый - это перевести смешанные числа в неправильную дробь и склмдывать их как дроби.
▪2-ой вариант - это надо сначала сложить целую часть, потом складываем дробную часть и после этого складываем полученные результаты при сложении целой и дробной частей
3. Что бы найти дробь от числа надо число умножить на эту дробь, т.е.
4. при умножении дробей надо перемножить числители и знаменатели этих дробей, т.е. умножение дроби на дробь дает дробь, числитель которой равен произведение числителей умножаемых дробей, а знаменатель равен произведению знаменателей умножаемых дробей
5. при умножении смешанных чисел сначала переводим их в неправильную дробь, а затем умножаем как дроби в п.4.
6. ----
7. что бы разделить дробь a/b на c/d надо делимое ( a/b ) умножить на число обратное делителю (d/c).
8. при деление смешанных чисел надо сначала их перевести в неправильную дробь а затем делить как в п.7
a = 4037, b = 8072, c = 16289295, d = 32586664
Тут, скорее, подойдёт метод пристального взгляда, с которого можно подобрать какие-то решения (это я к тому, чтобы не спрашивали, откуда взялись именно такие решения, всё методом проб и ошибок). Возьмём b = 2018k, d = ab, c ⋮ a, c / a = m. Тогда в первом уравнении получится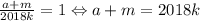
. Во втором уравнении получаем 
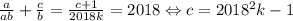. Чтобы легче было считать, возьмём k квадратом какого-нибудь числа. Если k = 1, то b = 2018, c = 2017 * 2019, a = 2017 или 2019. Уже отсюда видим, что a + m = 2017 + 2019 > 2018. Возьмём k = 4: b = 8072, c = 4035 * 4037, a = 4037 (оставим это), d = 4037 * 8072. Тогда для первого уравнения 
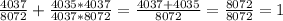- верно. Для второго: 
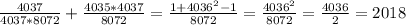- верно. Таким образом, четвёрка a = 4037, b = 8072, c = 4035 * 4037, d = 4037 * 8072 нам подходит.