Пусть ;так как данная дробь периодическая и бесконечна, то для неё верно: (*). Далее перепишем исходное уравнение в виде: х = 1 + А; подставляя это в (*), получим: ⇒ ⇒
A(1+2A) = 1 ⇒ 2A² + A - 1 = 0, откуда А = - 1 или А = 0,5. Второе значение положительно, оно и будет подходящим значением дроби .
Тогда А = 0,5 и х = 1 + 0,5 = 1,5 ⇒ 100х = 100·1,5 = 150 ⇒ [100x] = 150
Пусть ;так как данная дробь периодическая и бесконечна, то для неё верно:
;так как данная дробь периодическая и бесконечна, то для неё верно:  (*). Далее перепишем исходное уравнение в виде: х = 1 + А; подставляя это в (*), получим:
(*). Далее перепишем исходное уравнение в виде: х = 1 + А; подставляя это в (*), получим: 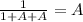 ⇒
⇒  ⇒
⇒
A(1+2A) = 1 ⇒ 2A² + A - 1 = 0, откуда А = - 1 или А = 0,5. Второе значение положительно, оно и будет подходящим значением дроби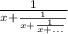 .
.
Тогда А = 0,5 и х = 1 + 0,5 = 1,5 ⇒ 100х = 100·1,5 = 150 ⇒ [100x] = 150
ответ: целая часть от 100х равна 150