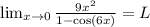Пошаговое объяснение:
lim(x->∞) (3x^2 - 4x + 1) / ( x - 2x^2 + 3) = lim(x->∞) (3 - 4/x + 1/x^2) / ( 1/x - 2 + 3/x^2) = (3 - 0 + 0) / (0 - 2 + 0) = - 3/2 = -1,5
lim(x->5) (x^2 - 7x + 10) / (x^2 - 25) = lim(x->5) (x - 2)(x - 5) / (x-5)(x+5) = lim(x->5) (x-2) / (x+5) = (5-2) / (5+5) = 3/10 = 0,3
3.
Пошаговое объяснение:
lim(x->∞) (3x^2 - 4x + 1) / ( x - 2x^2 + 3) = lim(x->∞) (3 - 4/x + 1/x^2) / ( 1/x - 2 + 3/x^2) = (3 - 0 + 0) / (0 - 2 + 0) = - 3/2 = -1,5
lim(x->5) (x^2 - 7x + 10) / (x^2 - 25) = lim(x->5) (x - 2)(x - 5) / (x-5)(x+5) = lim(x->5) (x-2) / (x+5) = (5-2) / (5+5) = 3/10 = 0,3
3.