22 открытки было подписано Верой за четвертый день
Пошаговое объяснение:
По условию задания Вера подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем.
Данная задача на арифметическую прогрессию. Количество дней, за которые выполнена работа – это количество членов прогрессии (n = 6), 640 открыток – это сумма всех членов прогрессии (S = 640), 10 открыток – это первый член прогрессии, т.е. а₁ = 10.
Применив формулу суммы членов арифметической прогрессии:
Sn = (2a₁ + d(n - 1)) * n
2
Мы можем найти d – разность арифметической прогрессии. Это число открыток, на которое Вера увеличивает свою норму в каждый следующий день:
640 = (2*10 + d(16 - 1)) * 16
2
640 = 20*8 + 15d * 8
640 = 160 + 120d
120d = 480
d = 480 : 120
d = 4
Т.е., каждый день Вера подписывает на 4 открытки больше, чем в предыдущий. Значит, за второй день она подписала 10 + 4 = 14 штук, за третий 14 + 4 = 18 штук, за четвертый 18 + 4 = 22 и т.д.
Количество подписанных открыток за четвертый день можно посчитать по формуле n-го члена прогрессии:
а₄= a₁ + d(4 - 1) = 10 + 4*3 = 10 + 12 = 22 (открытки) было подписано Верой за четвертый день.
Площадь первого прямоугольника равна 80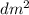
, второго - 44
.
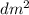Пошаговое объяснение:
Узнаем периметр второго прямоугольника:
1) 36 * 80% = 28,8 ( дм ) - периметр второго прямоугольника.
Узнаем удвоенную длину:
2) 10 * 2 = 20 ( дм ) - удвоенная длина.
Узнаем удвоенную ширину первого прямоугольника:
3) 36 - 20 = 16 ( дм ) - удвоенная ширина первого прямоугольника.
Узнаем удвоенную ширину второго прямоугольника:
4) 28,8 - 20 = 8,8 ( дм ) - ширина второго прямоугольника.
Узнаем ширину первого прямоугольника:
5) 16 : 2 = 8 ( дм ) - ширина первого прямоугольника.
Узнаем ширину второго прямоугольника:
6) 8,8 : 2 = 4,4 ( дм ) - ширина второго прямоугольника.
Узнаем площадь первого прямоугольника:
7) 10 * 8 = 80 (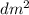
) - площадь первого прямоугольника.
Узнаем площадь второго прямоугольника:
8) 10 * 4,4 = 44 (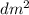
) - площадь второго прямоугольника.
22 открытки было подписано Верой за четвертый день
Пошаговое объяснение:
По условию задания Вера подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем.
Данная задача на арифметическую прогрессию. Количество дней, за которые выполнена работа – это количество членов прогрессии (n = 6), 640 открыток – это сумма всех членов прогрессии (S = 640), 10 открыток – это первый член прогрессии, т.е. а₁ = 10.
Применив формулу суммы членов арифметической прогрессии:
Sn = (2a₁ + d(n - 1)) * n
2
Мы можем найти d – разность арифметической прогрессии. Это число открыток, на которое Вера увеличивает свою норму в каждый следующий день:
640 = (2*10 + d(16 - 1)) * 16
2
640 = 20*8 + 15d * 8
640 = 160 + 120d
120d = 480
d = 480 : 120
d = 4
Т.е., каждый день Вера подписывает на 4 открытки больше, чем в предыдущий. Значит, за второй день она подписала 10 + 4 = 14 штук, за третий 14 + 4 = 18 штук, за четвертый 18 + 4 = 22 и т.д.
Количество подписанных открыток за четвертый день можно посчитать по формуле n-го члена прогрессии:
а₄= a₁ + d(4 - 1) = 10 + 4*3 = 10 + 12 = 22 (открытки) было подписано Верой за четвертый день.