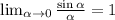Пошаговое объяснение:
Неопределённость 0/0. ⇒
Берём производную одновременно от числителя и знаменателя:
ответ: 2
===================
Пошаговое объяснение: используется первый замечательный предел:
Пошаговое объяснение:
Неопределённость 0/0. ⇒
Берём производную одновременно от числителя и знаменателя:
ответ: 2
===================
Пошаговое объяснение: используется первый замечательный предел: